ClarkVision.com

Crop Factor and Digital Cameras

by Roger N. Clark

All images, text and data on this site are copyrighted.
They may not be used except by written permission from Roger N. Clark.
All rights reserved.

Digital cameras have a large range of sensor sizes (e.g. Figure 1). Crop Factor refers to the size of the sensor in a digital camera relative to the size of the frame in a 35 mm camera. A 35 mm frame size is 24 x 36 millimeters (mm).

In order to give users some perspective on the effects of different sized sensors, photographers and camera manufacturers use a multiplication factor to illustrate to the user what the field of view a particular sensor has with certain lenses. When people were changing from 35 mm film to digital cameras with small sensors, it made sense to give focal lengths in the equivalent of what a 35 mm camera would give. If a digital camera sensor was half the size of a frame of 35 mm film, then the crop factor is said to be 2x. If you then used a lens with a focal length half that of what you used on the 35 mm camera, you would get the same field of view. For example, if you used a 50 mm lens on the 35 mm camera, then a 25 mm lens on the 2x crop camera would give the same field of view. This became known as the crop factor multiplier.

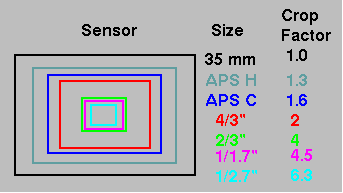
Figure 1. Various sensor sizes used in digital cameras. Depending on your monitor, the rectangles might be close to actual size or a little larger.

The crop factor effect is illustrated in Figure 2 with images of the Moon from 2 cameras. It appears that the camera with the 1.3x crop shows the Moon larger and thus with more detail. But Figure 3 shows the real story: in this case the full frame camera has the Moon larger with more pixels on the moon. The reason is that the number of pixels on the subject in an image has nothing to do with crop factor.

Figure 2. Crop factor effect of a 1.3x crop sensor (left) versus a full frame sensor using the same 500 mm lens. The images were obtained about a minute apart. Each image shows the entire frame as captured by each camera

Figure 3. The images from Figure 2 are scaled to 50% pixels (2 camera pixels for each screen pixel). The full frame sensor shows more pixels on the Moon because the pixel spacing is finer on the 5D Mark II than it is on the 1D Mark II.

The crop factor multiplier says that if you use a small sensor camera, then you can use smaller lenses and get the same field of view as larger lenses on the 35 mm camera. This seemed like a real boon to wildlife photographers and others wanting long telephoto lenses. For example, a 500 mm lens on a 35 mm camera has the same field of view as a 250 mm lens on a 2x crop camera. A 250 mm f/4 lens is a lot smaller than a 500 mm f/4 lens and costs many time less too. As I write this, web sites, photography news groups, and even camera manufacturer web sites say this focal length multiplier helps telephoto reach. One Zeiss web page even proclaimed a 280 mm f/5.6 lens was photographically equivalent to an 1800 mm f/5.6 lens! The idea is that the sensor has a crop factor of 6.43 and the lens has a 280 mm actual focal length and light gathering ability of an f/5.6 lens (it is an f/3.3 lens with 70% light loss from a beamsplitter: Zeiss web page on a new product: Photoscope, web page specifications as of October 18, 2009). The Zeiss web page goes on to say the Effective f-ratio is f4.0 @ 600mm, f5.6 @ 1800mm. This idea comes about from what is called the focal length multiplier. The idea is the cropped sensor sees a smaller field of view so it is like multiplying the focal length. The proponents of this idea is that this gives you more telephoto reach (more pixels on the subject). This idea is completely false. Crop factor does not give more reach, nor does it make a shorter focal length lens collect as much light as a greater focal length lens on a larger sensor. In this article I will try to set the record straight and debunk some of the myths regarding crop factor.

I will use subjects and examples that you can reproduce anywhere in the northern hemisphere of the Earth. The star Polaris and stars surrounding the north celestial pole can be images by people all over. An image of Polaris with a full-frame camera is shown in Figure 4.

Figure 4. A 30 second exposure of the star Polaris at ISO 800, with a Canon 5D Mark II, and a 500 mm f/4 lens from Erie, Colorado. The faint red sky is due to light pollution. We will focus this study on the small region around Polaris and the small star at the 1-o'clock position just above Polaris, as shown in Figure 5.

Figure 5. 100% crop of the region around Polaris. The image has been rotated so the second star is directly above Polaris.

Figure 6. Illustration of the focal length multiplier on the stars around Polaris. On the left is a 100% crop from a Canon 1D Mark II camera with a 1.3x crop sensor. On the right is a 100% crop from a canon 30D with a 1.6x crop sensor. The same lens was used for both images: a 500 mm f/4 lens with a 1.4x teleconverter giving 700 mm at f/5.6.

Some proponents of the crop factor multiplier would say the images in Figure 6 are just what one would expect from crop factor sensors. The smaller sensor seems to give more telephoto reach. But the same lens was used! The difference in Figure 6 has nothing to do with sensor size at all. The difference between the images is entirely due to pixel spacing, called pixel pitch. The Canon 1D Mark II has a pixel pitch of 8.2 microns, while the Canon 30D has 6.4 micron pixel pitch. The ratio of the pixel pitch is 8.2/6.4 so the spacing between stars is 1.28x compared to the sensor sizes 1.6/1.3 = 1.23. You can measure the star spacing yourself and see if the ratio of distances is 1.23 or 1.28. But the fact that these factors are close leads some to erroneously use crop factor as lens multiplier.

Lets look at a larger crop factor difference: a Canon 5D Mark II full frame sensor compared to a Canon 30D 1.6x crop sensor. If crop factor equals lens multiplier then the stars spacing in Canon 30D images should be spaced 1.6 times further apart as those in 5D Mark II images. Figure 7 shows the comparison. The two cameras recorded almost identical images at the pixel level. Of course, the full frame 5D Mark II camera recorded a larger field of view compared to the smaller sensor on the 30D. But both cameras show the same star spacing because the pixel pitch is the same in both cameras: 6.4 microns.

Figure 7. Comparison of a full-frame sensor and a 1.6x crop sensor using the same lens to image Polaris. On the left is a 100% crop from a Canon 5D Mark II camera with a 1.0x crop sensor (full frame). On the right is a 100% crop from a canon 30D with a 1.6x crop sensor. The same lens was used for both images: a 500 mm f/4 lens with a 1.4x teleconverter giving 700 mm at f/5.6. The spacing between stars is identical because the pixel spacings in the two cameras are the same.

Now let's look at light gathering ability. According to those who say the cropped sensor gives more telephoto reach, giving a focal length multiplier, the 700 mm f/5.6 lens on the Canon 30D should act like a 700 * 1.6 = 1120 mm lens at an "effective f/ratio" of f/5.6. A real 1120 mm f/5.6 lens would have an aperture area of 1120/5.6 = 200 mm compared to the 700 mm f/5.6 aperture of 700/5.6 = 125 mm. A 1120 mm f/5.6 lens would record stars 200*200/125*125 = 2.56 times fainter.

The stars recorded by the 5D Mark II and 30D cameras are compared in Figure 6. Both cameras recorded the same faint stars. The 1.6x crop camera (30D) did not record fainter stars, especially 2.56 times fainter (a little more than one stellar magnitude). Indeed, if the crop sensor recorded fainter stars, then simply cropping the image on the 5D Mark II would suddenly show fainter stars, a preposterous idea.

Figure 8. Images from Figure 7 with hot pixels circled. On the left is a 100% crop from a Canon 5D Mark II camera with a 1.0x crop sensor (full frame). On the right is a 100% crop from a canon 30D with a 1.6x crop sensor. The same lens was used for both images: a 500 mm f/4 lens with a 1.4x teleconverter giving 700 mm at f/5.6. Both cameras recorded the same faintest stars, and example is shown by the arrow. Compare stars in the two images and ignore the circled hot pixels.

Crop factor has nothing to do with telephoto reach. Crop factor its associated focal length multiplier only applies to the field of view and focal length that would give the same fields of view on cameras with different sized sensors.

The controlling factor in telephoto reach is "pixels on subject," and that is controlled by 2 variables: real focal length, and pixel pitch.

You can compute the size of a subject in your image by using the concept known as plate scale.

plate scale = 206265 * pixel pitch / focal length

The 206265 constant is the number of arc seconds in one radian and the equation applies to small angles as one would encounter with telephoto lenses. To compute sizes in a wide angle image requires trigonometry and tangents.

For example with the 700 mm focal length used in Figures 7 and 8, and the 6.4-micron pixel pitch, the plate scale is:

5D Mark II 700mm plate scale = 206265 arc-seconds * (6.4 microns /1000 microns/mm) / 700 mm = 1.8 arc-seconds/pixel.

Now if you know the size of your subject, you can compute the size in pixels:

subject size in pixels = size in arc-seconds / plate scale.

The moon, for example, is about 1800 arc-seconds in diameter, so it would appear 1800 / 1.8 = 1000 pixels in diameter in 5D Mark II and 30D images with the 700 mm lens.

If you know the size of a subject and its distance, you can compute its apparent size in arc-seconds:

subject angular size = 206265 * subject size / subject distance.

For example, a 0.5 meter bird at 50 meters appears: 206265 * 0.5 / 50 = 2063 arc-seconds across, about the size of the Moon. The Canon 30D with a 700 mm lens would make an image of the bird 2063 / 1.8 = 1146 pixels.

Conclusions

Crop factor and the associated focal length multiplier only affects field of view. They do not affect telephoto reach.

Effective focal ratio is a bogus concept. A cropped sensor does not suddenly multiply the lens focal length with the same f/ratio.

Examples: A 100 mm f/2 lens on a 10x crop sensor does not magically become the photographic equivalent of a 1000 mm f/2 lens on a 35 mm camera. If you see a camera or lens manufacturer make such claims, it is false advertising. Pixel pitch and real focal length are the key variables that control telephoto reach, assuming the lens and sensor can actually resolve the detail. For example, a sensor with 1.8 micron pixels and an f/8 lens does not resolve detail at the 1.8 micron spacing because an f/8 lens can't resolve detail finer than about 5 microns (it varies a little from blue to red light). So telephoto reach actually needs 3 variables: real focal length, pixel spacing, and lens resolution that can deliver the resolution at the sensor pixel pitch.

Additional Reading

Digital Cameras: Does Pixel Size Matter? Factors in Choosing a Digital Camera (Does Sensor Size Matter?) Good digital cameras are photon noise limited. This sets basic properties of sensor performance.

The f/ratio Myth and Digital Cameras.

Etendue, or Optical Throughput.

Home Galleries Articles Reviews Best Gear Science New About Contact

http://www.clarkvision.com/articles/cropfactor

First Published October 18, 2009
Last updated November 14, 2009.