
Digital Cameras:
Counting Photons, Photometry, and Quantum Efficiency
by Roger N. Clark
All images, text and data on this site are copyrighte
d.
They may not be used except by written permission from Roger N. Clark.
All rights reserved.
Introduction
Modern digital cameras are wonderful light measuring devices, capable
of measuring a few photons, being limited by photon statistics and
a small amount of read noise.
By averaging multiple frames, the already small read noise can be
virtually eliminated with the noise in the resulting measurement
limited by photon noise (Poisson statistics). This means that digital
cameras can be used to measure a variety of properties, from
their own performance, to precision measurements of other objects.
Traditional photographic light meters are calibrated in ISO speed,
f/stops and shutter speeds, but by recording raw data from digital
cameras, the fundamental counting of photons
can be accomplished. From the number of photons, and their
wavelength, recorded through the 3 color filters, measurement of power
can be calculated for those colors. This page describes
how some of these quantities can be determined.
How many photons are incident on the earth and recorded by cameras?
Using calibrated light sources, one can derive a number of properties
about a camera. But you need not purchase an expensive standard light
source because there are many standards freely available to everyone:
stars. Stars range in brightness from the super intense light from
our own sun, to the stars in the night sky, covering a total range
impossible to achieve with any single commercial or research standard.
Fortunately, many stars, including our sun, have been meticulously
calibrated over many years. We start by using light measured from
the star Alpha Lyra.
Using the reference star Alpha Lyra, we can calibrate
the signal a camera records in photons.
Alpha Lyra radiates 3.7x10-8 watts per square meter
per micron (wavelength interval) above the atmosphere of the Earth
(Oke and Schild, 1970, Schild et al., 1971),
at a wavelength of 0.53 micron (5300 angstroms) (Figure 1), the central
wavelength of the green filter in a Canon 10D digital camera.
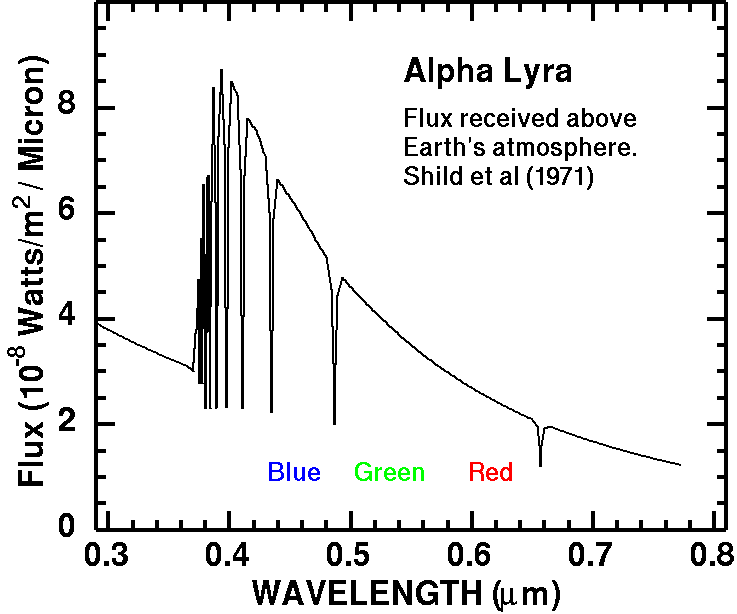
Figure 1. Alpha Lyra Spectrum from Schild et al. (1971).
EAlpha Lyra = 3.7x10-8 w/m2 micron (eqn 1)
The energy of a photon is
Ephoton = h*c/lambda, (eqn 2)
where h is the Planck constant 6.626x10-34 J-s,
c is the speed of light, 2.997925x108 meters/second,
and lambda is the wavelength of light. J is Joule. One watt is one
J/second.
Therefore, the energy of a 0.53 micrometer photon = 3.7x10-19 J.
Dividing the results for Alpha Lyra from equation 1 by equation 2,
we find the number of photons Alpha Lyra shines on the Earth,
above the atmosphere is 1x1011 photons/m2/s/micron
(photons per square meter per second per micron).
Now we need to know the wavelength range to be considered.
The bandpass, called the Full Width at Half Maximum, or FWHM
is 0.077 microns for the green filter of the Canon 10D camera
(other digital cameras are probably very similar).
The number of Alpha Lyra photons collected through a
perfect green filter would be 1x1011 * 0.077 = 7.7x109
photons/m2/s (7.7 billion photons per square meter per
second).
There is absorption through the atmosphere, which is variable
depending on sky conditions, but from a good clear sky a little
above sea level, absorption in the green passband is only about 15%
when the star is viewed overhead.
So the number of photons reaching the Earth's surface in such
conditions is about 6.5x109 photons/m2/s.
I aimed a 500 mm f/4 telephoto lens plus a 1.4x teleconverter
at Alpha Lyra when it was overhead and took a series
of exposures with a Canon 10D digital camera. The camera recorded the
raw data to the memory card, and I converted the data using a linear
conversion in ImagesPlus 2.5. The camera's blur filter, its
focus, and atmospheric
turbulence smeared the starlight over several pixels, so the
total signal was the sum of all pixels containing star light minus
an equal number of surrounding pixels summed to measure the sky
background. From this I determined in a 1/90 second exposure at ISO
400, that all pixels with Alpha Lyra signal totaled
503,700 DN (integer Data Numbers). (No one pixel recorded more than
the 65,535 16-bit DN limit.) Scaling that value to the total
expected in a one second exposure we should see 45,300,000 DNs.
A 500 mm f/4 lens has an aperture of 125 mm in diameter which is
0.0123 m2 (square meters). From the flux of Alpha Lyra
photons, we calculate that there would be about 6.5x109
* 0.0123 = 80,000,000 photons/second through the green passband.
Since we observe 45,300,000 DNs, this means that one DN in the
16-bit linear file is 80,000,000/45,300,000 = 1.77 photons/DN at ISO
400. The original camera digitization is 12-bit, so this same scale
is mapped into 0 to 4095 instead of the 16-bit 0-65,535, a factor of
16. Thus, there are 1.77*16 = 28.3 photons/camera DN at ISO 400.
Quantum Efficiency of the Canon 10D Sensor
The measured DN's from Alpha Lyra and calculated photons allow
us to calculate the system efficiency, called T*QE here. The
system throughput, T, is the transmission of all optics from the lens
to the blur and Bayer filter over the sensor times the fractional
active area of the sensor's pixels.
The calculated Alpha Lyra photons entering the 125 mm aperture
lens is 80,000,000 photons/second.
The measured DN is 45,300,000 DN/second. But this is 16-bit computer
file DN. Camera DNs are 16 times less, or 2,830,000 12-bit camera
DN/second. The gain, determined here
is 2.7 electrons/DN (12-bit camera DN). Thus the number of
photons actually detected is 2,830,000 * 2.7 = 7,640,000
photons/second. Since we expected 80 million, and observed
only 7.64 million, the system T*QE = 7.64/80 = 0.095 or 9.5%.
The transmission of a lens is variable, depending on the coatings
and number of elements. The 500 mm f/4 lens has 17 elements.
If each lens surface is multi-coated and transmits 99%
of the light, the lens would transmit 0.9934 = 71%.
The 1.4x teleconverter would transmit about 90% of the light, so we
are down to 64% of the light transmitted through the lens system.
Next the blur filter, another loss of about 2%, then the Bayer
filter. The green filter peak probably has a maximum transmittance
of 90% based on my experience with similar filters (this is very
optimistic)(see Reference 10).
So we are down to system transmission of 0.71*0.9*0.98*0.9 = 0.56 or 56%.
The fill factor of the sensor is the percentage of the sensor
that is sensitive to light. originally I assumed 80% (the true value is perhaps
as low as 25%, but a microlens concentrates the light boosting the effective
fill factor). But newer camera models (see the 1D Mark II fill factor
below) help constrain fill factors. The 10D, being older technology than
the 1D mark II is likely slightly less. The 1D II fill factor is less than
0.77, and likely around 0.69, so the 10D fill factor is probably closer
to 0.65.
Thus, a system transmission of 56% times the fill factor, means
only about 36% of the light entering the
lens is actually incident on the sensitive area of the
detector. For the Alpha Lyra test, this would be 80,000,000 * 0.36 =
29,000,000 photons /second incident onto the detector's sensitive area.
Since we measured 7,640,000 photons were measured per second, the
device quantum efficiency over the green passband is 7,640,000 /
29,000,000 = 0.26. The quantum efficiency of the 10D over the
green filter bandpass is QE = 26%. This is very similar to
QE of about 19 to 26% reported for CMOS detectors (References 3, 4, 5, 6,
7).
Quantum Efficiency The Canon 1D Mark II Sensor
The introduction of the Canon 1D Mark III camera helps us place
limits on the fill factor of the 1D Mark II sensor. Canon stated
that the 1DIII pixels collects the same amount of light as do the
1DII pixels. The 1DIII pixel pitch is 7.2 microns and the 1DII
is 8.2 microns, for an area ratio (1DIII/1DII) of 0.77. Thus the
1DII fill factor = 0.77 * the 1DIII fill factor. Assuming the
fill factor of the 1DIII = 0.9, then the 1DII = 0.9*0.77 = 0.69.
Analyzing data for the Canon 1D Mark II camera using the same lens to measure
the photons received from Alpha lyra, I measured a total signal of 1,173,396 DN
counts in 1/100 second at ISO 800. That translates to 11,953,972 photons/second
through the greem filter. The expected light from Alpha Lyra was 80,000,000
photons/second, so the T*QE = 11,953,972/80,000,000 = 0.15 or 15%, which is over
50% better than the canon 10D. If we assume similar numbers for optical transmission
as above (71% for the 500 mm lens, 90% for the TC, 98% for the blur
filter, and 90% for the green filter), and 69% for the fill factor
(due to better micro lenses), T = 0.40 and the QE is found to be 38% through
the green passband. This is a very similar number to that reported for CMOS detectors
(References 3, 4, 5, 6, 7), but on the high end compared to older references
(one might expect a small improvement in QE with newer technology).
Typical Photons/Pixel in a Typical Picture
From the above, we can estimate the number of photons in a typical
picture for the Canon 10D camera. Assuming that a 100% reflectance
target gives a maximum response in a 16-bit output file, 65,535
then in linear units, an 18% gray card would give 0.18*65535 =
11,800 DN (remember this is a linear scale). From the
gain in electrons/DN =2.7, from
here we get the
following, assuming all lenses behave similar to the transmission
factor of the canon 500 mm f/4 L IS lens (a good multi-coated lens),
Table 1: Canon 10D Photon Information, green filter with T*QE of 9.5%
| Photons incident
on detector Package | Photons Detected | |
| ISO | Photons/16-bit
Linear DN |
Photons/12-bit
Camera DN |
Photons/12-bit
Camera DN | 18% Gray Card
Number of
Photons |
Energy
(Joule) |
| 100 | 7.06 | 113 | 11 | 7,900 | 2.9x10-15
|
| 200 | 3.52 | 56 | 5 | 4,000 | 1.5x10-15
|
| 400 | 1.77 | 28 | 2.7 | 2,000 | 7.3x10-16
|
| 800 | 0.88 | 14 | 1.3 | 990 | 3.6x10-16
|
| 1600 | 0.44 | 7 | 0.7 | 490 | 1.8x10-16
|
| 3200 | 0.22 | 3.5 | 0.3 | 250 | 9.1x10-17
|
Note: Camera A-D converter numbers are typically 12-bit, so are a factor of 16
different from 16-bit DNs. Thus Photons/12-bit camera DN is 16 times
greater than in the above photons/16-bit linear DN. For example,
at ISO 100, each raw camera 12-bit DN represents 7.06*16 = 113
photons.
Computing power from Joules: divide by the exposure time to get watts.
For example, if you take a picture with an exposure time of 1/100 second,
camera needs only 2.9x10-17 watts from the 18% gray card
(0.029 millionth of one billionth of one watt!) per pixel.
Camera saturation levels are 5.5 times larger than the above 18% gray card
levels. Energy incident is about 10 times higher than the values above.
Detecting Very Faint Signals from Astronomical Objects
The Stellar Magnitude Brightness Scale
Now that we have calibrated a digital camera using the 0-magnitude
star Alpha Lyra, we can calculate the signal from other astronomical
objects. The brightnesses of astronomical objects is measured in
stellar magnitudes, with Alpha Lyra forming a reference = 0 at
all wavelengths. The magnitude is a log scale with one magnitude
equal to the fifth root of 100, or 2.51188643, and large numbers
mean fainter. The table below shows the relative brightness scale
and common subjects (derived from Clark, 1990).
Table 2
Stellar Luminance at Camera
Magnitude Earth's surface Exposure
(lumens/sq. meter) Time on 18%
(lux) gray card
Sun overhead -26.7 130000 1/600s f/8 ISO100
Full daylight (not direct sun) -24 to -25 10000-25000
Overcast day -21 1000 1/4s f/8 ISO100
Very dark overcast day -19 100 1/4s f/4 ISO200
Twilight -16 10 1s f/4 ISO400
Deep twilight -14 1 3s f/2 ISO400
1 Candela at 1 meter distance -13.9 1.00 3s f/2 ISO400
Full Moon overhead -12.5 0.267 3s f/2 ISO1600
First or Last Quarter Moon, overhead -10.0 0.027 30s f/2 ISO1600
Total starlight + airglow -6 0.001 775s f/2 ISO1600
Venus at brightest -4.3 0.000139
Total starlight at overcast night -4 0.0001 970s f/1 ISO3200
Sirius -1.4 0.0000098
0th-mag star 0 0.00000265
1st-mag star +1 0.00000105
6th-mag star +6 0.0000000105
A camera's light meter can be used to measure lux. The formula is
comes from the definition of ISO (References 11, 12):
lux = 12.4 * pi * f/#2 / (R * t * exposure_time * ISO), (eqn 3)
where f/# is the f/number of the camera lens, exposure time is
in seconds, ISO is the ISO speed, R = reflectance of the target,
t = lens transmission, and pi = 3.14159. The constant 12.4 varies
with different light meters, so the equation is approximate.
The constant can vary from 10.6 to 13.4 and have been reported
as high as 17 (See References 11, 12).
Equation 3 can be simplified with some assumptions. If we assume
white paper with 90% reflectance (use a stack of several sheets),
R = 0.9, and assume the opticat transmission, T = 0.7, then
Equation 3 reduces to:
lux = 62 * f/#2 / (exposure_time * ISO), (eqn 4)
For example, I measured the exposure time on white paper in full
sunlight at 1/3000 second at f/8, ISO 100. Equation 4 gives
the lux from the sun as 119,000, agreeing within 10% of the value in
the above table. If you want to use an 18% gray card, the factor
62 becomes about 310.
Table 3 The Magnitude Scale
| magnitude | Relative
intensity | example |
| -26.5 | 40,000,000,000. | The Sun |
| -21 | 251,000,000. | Overcast day |
| -13.9 | 363,000. | 1 Candella at 1 meter |
| -12.5 | 100,000. | Full Moon |
| -10 | 10,000. | |
| -8 | 1,584. | |
| -7 | 631. | |
| -6 | 251. | Total of all starlight |
| -5 | 100. | |
| -4 | 39.8 | Total of overcast starlight |
| -3 | 15.8 | |
| -2 | 6.31 | |
| -1 | 2.51 | |
| 0 | 1.000 | Alpha Lyra |
| 1 | 0.398 | |
| 2 | 0.160 | |
| 3 | 0.0631 | |
| 4 | 0.0251 | |
| 5 | 0.0100 | |
| 6 | 0.00398 | 6th magnidute star, faintest star many people can see |
| 7 | 0.00158 | |
| 8 | 0.000631 | |
| 9 | 0.000251 | |
| 10 | 0.000100 | |
| 15 | 0.000001 | |
| 20 | 0.00000001 | |
| 22 | 0.0000000016 | Faint dark sky
|
| 23 | 0.00000000063 | |
| 24 | 0.00000000025 | |
How faint can a DSLR detect? With the Canon 10D, a 500 mm f/4 lens
plus a 1.4x TC, giving 700 mm at f/5.6, the camera plus lens sees
a patch of sky 3.1 arc-seconds in size (the 10D has 6.2-micron
pixels). Nebula have been measured
(click here for an example) with a surface brightness around magnitude
23 per square arc-second. With 3.1 micron pixels, about 7.5 square
arc-seconds assuming an 80% fill factor for the sensor, the Canon 10D
receives 80,000,000 photons/sec * 0.00000000063 *7.5 = 0.4
photons/second at the entrance to the 5-inch aperture lens.
In a 1-minute exposure, that would be only 23 photons! But the lens
absorbs, as does the filters, so with the system throughput of T*QE = 9.5%,
the sensor would detect only about 2.2 photons per pixel in a 1-minute
exposure. Note this detection was done under skies with strong light
pollution from the city of Denver contributing about 350 photons
per pixel per minute. The photon noise from the sky was
about 18.7 per frame. Multiple exposures amounting to about
40 minutes of time reduced the sky noise to about 3. Forty
exposures of the 2.2 photons/pixel object gave 88 photons
with a photon noise of 9, so the noise from the sky is not
dominant at that brightness in the multiple exposure average.
This demonstrates measuring signals much lower than the noise, in
this case a factor of about 160 times smaller!
References
1) Oke, J.B. and Schild, R.E., The Absolute Spectral Energy Distribution
of Alpha Lyrae, Astrophysical Journal 161, p 1015, 1970.
2) Schild, R.E., Peterson, D.M., and Oke, J.B., Effective Temperatures
of B- and A- Type Stars, Astrophysical Journal 166, p
95, 1971.
3)
James Janesick, Charge coupled CMOS and hybrid detector arrays
SPIE, San Diego, Focal Plane Arrays for Space Telescope, paper
#5167-1, Aug 2003.
http://huhepl.harvard.edu/~LSST/general/Janesick_paper_2003.pdf
4) Introduction to CMOS Image Sensors (Figure 4 has CMOS transmission
curves).
A CMOS Camera manual, See Figure 1-2 for QE spectral response
including Bayer filter transmission. March 22, 2004.
6) Global Computer Vision.
Page 17 shows Bayer filter spectral response.
7) CMOS image sensors:
ECLIPSING CCDs in visual information? 1997
(Figure 3 has spectral information, Table 2 has QE information.)
8) Radiometry and photometry in astronomy
By Paul Schlyter, Stockholm, Sweden.
9) Clark, R.N., Visual Astronomy of the Deep Sky, Cambridge
University Press and Sky Publishing, 355pp., 1990.
10) http://www.ifa.hawaii.edu/~wang/misc/QE.jpg 4 plots:Canon 20D QE, Ir
filter, Bayer filter, total. At 0.53 micron: QE = 50%, IR filter
transmission = 93%, green filter = 88%, for QE*IR*G = 41%.
11) Using a camera as a lux meter
12) International Standard ISO 2720: Photography - General purpose
photographic exposure meters (photoelectric type) - Guide to product
specification. First edition 1974.
13) Comparative Test Canon 10D / Nikon D70
in the Field of Deep-Sky Astronomy, including spectral response.
Home Page: ClarkVision.com
Back to:
Digital Camera Sensor Analysis pages on this site:
http://clarkvision.com/articles/index.html#sensor_analysis
http://clarkvision.com/articles/digital.photons.and.qe
First published January 22, 2006.
Last updated January 4, 2013
