ClarkVision.com
| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
Telephoto Reach and Digital Cameras, Part 1
by Roger N. Clark
| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
by Roger N. Clark
Introduction
Given a distant subject that will be small in your picture, what do you need to maximize detail on the subject for a given set of cameras and lenses? Obviously, more focal length helps, but that is not the only answer. For example, say you only had a 300 mm lens, and 2 cameras to choose from, a full-frame DSLR and a DSLR with a 1.6x crop factor sensor? The answer to this question needs more information as crop factor has nothing to do with detail on a subject that is small in the frame in these focal length limited situations. The answer is the camera with the smaller pixels. But even then the best solution is not obvious.
Our Moon is used as examples in this article. The reason is you can use your own lens and cameras to test the lenses and your technique. If you image the Moon with your equipment, are you able to match of exceed the detail shown here at similar focal lengths?
High-End Fixed Focal Length versus Consumer Zoom Lenses
Amateur photographers usually buy consumer zoom lenses with the hope that the low cost lens will enable them to get great images of distant subjects, whether wildlife or sports. Figure 1 illustrates the difference between a low cost consumer zoom and a quality fixed focal length lens. Clearly, lens quality has a major impact on the resolution one is able to record at a given focal length. Another way to look at the results in Figure 1 is that one only needs a much shorter focal length quality lens to deliver the detail of a much longer focal length soft lens.
Lesson 1: use the best lenses you can afford, and more focal length is not always the best solution.

Figure 1. Comparison of images of the moon with a high-end
fixed focal length lens (300 mm f/4 L IS) versus a low
cost consumer zoom. The consumer zoom has very poor image quality
at its fastest f/ratio (f/5.6), and improves a little at f/8.
In contrast, the L lens is very sharp at its fastest
f/ratio, sharper than the consumer zoom at f/8. The L lens
has is not only sharper at f/4 than the zoom at f/8, but that
gives a two stop advantage to freeze motion, and the ability
to get better images at lower light levels.
Pixel Pitch Makes a Difference
There is a huge range of digital cameras to choose from these days, including excellent used cameras no longer in production. For a given focal length, the spacing from one pixel to the next (the pixel pitch) determines how much fine detail may be sampled. Assuming the lens delivers the detail, smaller pixels will record that detail. Figure 2 illustrates this effect. The same lens was used on 4 different DSLRs with pixel pitches from 8.4 microns to 4.3 microns.
There is a downside to smaller pixels. For a given lens, e.g. the 300 mm lens in Figure 2, the same amount of light is delivered to each square mm in the focal plane. This means that if you pack more pixels in each square mm, then each pixel must get less light in a given exposure time. An analogy is cutting up a pie into more pieces means each piece must be smaller, thus containing less pie. So there is a trade: finer detail versus more noise. But if you have enough light then noise is not objectionable and we see this effect in Figure 2.
Lesson 2: smaller pixels can deliver more detail in an image, at the expense of more noise per pixel. A corollary to this lesson is that if you want to maintain signal-to-noise ratio, you need a larger aperture lens to deliver the light to the smaller pixels.

Figure 2. The Moon photographed with 4 different cameras using
the same lens, so focal length is the same for each image.
This is the full resolution image produced in the camera
and written as a jpeg file. No post processing sharpening has been
done.
Wildlife Photography
In wildlife photography, photographers often strive to get closer, but still can not get close enough to fill the frame with the subject. So photographers add teleconverters (TCs) to increase focal length. With a quality lens and a quality teleconverter, the image can still remain very sharp. Let's work a real example.
I have traveled to the African Serengeti to photograph the wildlife with a 500 mm f/4 telephoto lens. This lens is very sharp and works very well with 1.4x and 2x teleconverters (many examples can be found in the galleries). Such a big lens has a great advantage with the focal length, but a big disadvantage because it is so bulky and heavy, it can be difficult to move quickly to catch the action. So for my next trip, I want a smaller lighter lens for the easier handling, but I do not want to give up detail that I could have gotten with the 500 mm. However, I am comfortable with the detail the 500 mm lens delivered on previous trips. Could I achieve my goals with a 300 mm f/2.8 lens?
On my previous trips with the 500 I had a Canon 10D, 1D Mark II, and 5D Mark II cameras. The characteristics of these cameras are:
Table 1
Camera mega- crop pixel pitch Slowest f/ratio
Model pixels factor (microns) for autofocusing
Canon 10D 6.3 1.6 7.4 5.6
Canon 1D Mark II 8.2 1.3 8.2 8
Canon 5D Mark II 21.1 1.0 6.4 5.6
Some other cameras for comparison:
Canon 30D 8.2 1.6 6.4 5.6
Canon 1D Mark III 10.1 1.3 7.2 8
Canon 1D Mark IV 10.1 1.3 5.7 8
Nikon D3 12.1 1.0 8.46
Nikon D3s 12.1 1.0 8.46
Nikon D7000 16.2 1.5 4.8
The smallest detail on a subject is given by the plate scale, a concept that originated back in the days of photographic glass plates. We want to detect the smallest angular size, and that is given by the equation: plate scale = pixel pitch / focal length, where the pixel pitch is expressed in mm (0.001 mm = 1 micron) and the result is in radians. Perhaps an easier number is arc-seconds. The moon is about 1800 arc-seconds in diameter and 1 arc-second is about the smallest amount of detail that can be seen through the Earth's atmosphere (sometimes a little better, sometimes a little worse). The plate scale in arc-seconds/pixel is:
plate scale = 206.265 * pixel pitch in microns / focal length in mm.
There are 206265 arc-seconds in one radian, and the 206.265 factor is the 206265 / 1000 (microns per mm).
Here is the plate scale achieved with a 500 mm lens, and teleconverters, with the above cameras.
Table 2
Camera Lens focal Tele- Total f/ratio pixel Plate Scale Diffraction/pixel
Model length converter focal pitch (arc-seconds limited
(mm) length (microns) per pixel) (0% MTF)
(mm) (arc-seconds)
Canon 10D 500 none 500 4 7.4 3.1 3.1
Canon 10D 500 1.4x 700 5.6 7.4 2.1 2.1
Canon 10D 500 2x 1000 8 7.4 1.5 (NO AF) 1.5
Canon 1D Mark II 500 none 500 4 8.2 3.4 3.4
Canon 1D Mark II 500 1.4x 700 5.6 8.2 2.4 2.4
Canon 1D Mark II 500 2x 1000 8 8.2 1.7 1.7
Canon 5D Mark II 500 none 500 4 6.4 2.6 2.6
Canon 5D Mark II 500 1.4x 700 5.6 6.4 1.9 1.9
Canon 5D Mark II 500 2x 1000 8 6.4 1.3 (NO AF) 1.3
NO AF = no autofocus.
Note: when the diffraction limit = plate scale, the system is pixel spacing limited.
Another factor in actual recorded detail is the strength of the blur filter in each camera. The blur filter in the 1D Mark II camera is pretty strong, so that the 5D Mark II with a 1.4x TC on the 500 mm lens actually gives more detail than the 1D Mark II with a 2x TC. Notice crop factor has nothing to do with fine detail.
So for my next trip, I need to maintain a plate scale of about 1.7 arc-seconds/pixel with a choice of a couple of cameras (I've also included some other cameras for comparison):
Table 3
Camera mega- crop pixel pitch Slowest f/ratio
Model pixels factor (microns) for autofocusing
Canon 30D 8.2 1.6 6.4 5.6
Canon 1D Mark IV 16.1 1.3 5.7 8
Canon 7D/60D/T2i 17.9 1.6 4.3 5.6
Nikon D3 12.1 1.0 8.46
Nikon D3s 12.1 1.0 8.46
Nikon D7000 16.2 1.5 4.8
So how do these cameras compare to the previously used cameras. Note the 30D has the same pixel pitch as the 5D Mark II, so produces about the same fine detail on a subject. But the 1D Mark IV has smaller pixels so a shorter focal length lens might do the job.
Table 4
Camera Lens focal Tele- Total f/ratio pixel Plate Scale Diffraction/pixel
Model length converter focal pitch (arc-seconds Limited
(mm) length (microns) per pixel) (0% MTF)
(mm) (arc-seconds)
Canon 1D Mark IV 300 none 300 2.8 5.7 3.9 3.9
Canon 1D Mark IV 300 1.4x 420 4 5.7 2.8 2.8
Canon 1D Mark IV 300 2x 600 5.6 5.7 2.0 2.0
Canon 1D Mark IV 300 2x + 1.4x 840 8 5.7 1.4 1.4
Canon 7D/60D/T2i 300 none 300 2.8 4.3 3.0 3.0
Canon 7D/60D/T2i 300 1.4x 420 4 4.3 2.1 2.1
Canon 7D/60D/T2i 300 2x 600 5.6 4.3 1.48 1.48
Nikon D7000 300 none 300 2.8 4.8 3.3 3.3
Nikon D7000 300 1.4x 420 4 4.8 2.4 2.4
Nikon D7000 300 2x 600 5.6 4.8 1.65 1.65
Note: when the diffraction limit = plate scale, the system is pixel spacing limited.
The above table shows that the Canon 1D Mark IV with a 300 mm f/2.8 lens with stacked 2x and 1.4x TCs can achieve a plate scale greater than the cameras and lens combinations in Table 2 that still maintain autofocus. But can stacked TCs actually deliver the image quality? Figure 3 shows the results, and the clear answer is yes.
The Canon 7D comes a close second. Note that the 1D Mark IV needs the next higher TC to closely match the plate scale of the 7D (e.g. case 1: 1DIV + 300mm + 2x TC gives similar plate scale as the case 2: 7D + 300 mm + 1.4x TC). Which gives better noise, case 1 or case 2? In fact the noise per pixel would be almost identical! That is because the same aperture lens is delivering the almost same amount of light to each pixel, and both sensors have similar sensitivity.
Lesson 3: While lens quality, focal length and pixel pitch are all factors in telephoto reach, when you need to maintain autofocus, the camera body and its ability to autofocus with different teleconverters is an important consideration.

Figure 3. Comparison of images of the moon with different camera
and lens combinations. The images are sorted with the combination
delivering the most detail on the left, although the differences
in the right-most 3 images are small.
Click here for full resolution.
Point and Shoot Super Zoom Cameras
Consumer super zoom cameras have the illusion of delivering an "equivalent focal lengths" as long as telephoto lenses on 35-mm format cameras. For example, consider a Canon SX20IS, which has a 20x zoom lens ranging from 28 to 560mm (35mm equivalent). But 35 mm equivalent means field of view, not actual resolved detail.
The SX20IS has a 12.1 megapixel sensor with 1.54 micron pixels. The actual lens focal length is 5 to 100 mm. That means the smallest angular size of one pixel is 206265 * (1.54/1000)/100 = 3.2 arc-seconds. In Table 4, above, we saw that a Canon 7D plus a 300 mm lens beats that specification, and Figure 2 shows the 7D + 300 mm fixed focal length lens delivers incredible sharpness. The SX20IS is f/5.7 at its longest zoom and diffraction alone smears the detail by more than 2 times so the super zoom is no contest for the image quality of the DSLR.
Specifications for some super zoom cameras are listed in Table 5. A key factor in actual resolution on a target is diffraction. Diffraction is the major limiting factor in point and shoot super zoom digital cameras due to the small pixel sizes, and this is assuming the zoom lenses were perfect (and they are not). The point at which diffraction reduces resolution to zero (called 0% Modulation Transfer Function, MTF) is near 4 microns (varies from a little lower in blue light to a little larger in red light). The small pixels in super zoom digital cameras are currently much smaller than 4 microns, so all of those cameras can not achieve the resolution implied by the pixel size. The only way to beat this problem is larger pixels (greater than about 4 microns) and longer true focal length lenses, while maintaining a reasonably fast f/ratio. This is the realm of DSLRs.
Add to the faster response of a DSLR with its phase detect autofocus system, the faster apertures available, and the better low light performance, the DSLR with modest telephoto lens far surpasses a point and shoot super zoom camera for photography of distant subjects, including wildlife, sports, and astrophotography. Of course, the DSLR costs more and weighs more. Image quality differences between a P&S superzoom and a DSLR is shown in Figure 4.
Table 5
Pixel 35 mm True f/ Angular Pixel Diffraction/pixel
Pitch equivalent focal ratio Size at max Limited
(microns) field-of-view length at max focal length (0% MTF)
Mega focal length (mm) focal (arc-seconds) (arc-seconds)
camera Model Pixels (mm) length (perfect lens)
----------------------------------------------------------------------------------------------
Canon 7D/60D/T2i 18 4.3 960 600 5.6 1.48 1.48 (pixel limited)
+300mm
f/2.8
+2x TC
Canon 7D/60D/T2i 18 4.3 672 420 5.6 2.1 2.1 (pixel limited)
+300mm f/4
+1.4x TC
Nikon D7000 16.2 4.7 900 600 5.6 1.65 1.65 (pixel limited)
+300mm
f/2.8
+2x TC
Canon SX30IS 14 1.43 24-840 4.3-150.5 5.8 1.96 4.5 (diffraction limited)
Panas- FZ50 10 1.97 35-420 7.4-88.8 3.7 4.6 4.8 (diffraction limited)
onic
Panas- FZ35 12 1.53 27-486 4.8-86.4 4.4 3.6 5.9 (diffraction limited)
onic
Canon SX20IS 12.1 1.54 28-560 5-100 5.7 3.2 6.6 (diffraction limited)
Fuji HS20EXR 16 1.4 24-720 4.2-126 5.6 2.3 5.6 (diffraction limited)
----------------------------------------------------------------------------------------------
Notes:
Diffraction limit assumes the lens is perfect and not limited by other aberrations,
but most zoom lenses are not diffraction limited at their widest apertures,
as illustrated in Figure 1.
When the diffraction limit = plate scale, the system is pixel spacing limited.
Diffraction limit for green light, red light would be worse by ~30%
FZ35 = 4000 x 3000 pixels in a 6.13 x 4.60 mm sensor
SX30 = 4320 x 3240 pixels in a 6.2 x 4.6 mm sensor
----------------------------------------------------------------------------------------------
Lesson 4: If your desire is to make top quality wildlife photos, a DSLR is the way to go. The clear apertures of super zoom lenses on so called point and shoot digital cameras are too small to deliver fine detail as they are diffraction limited at best.

Figure 4. Comparison of images of the moon with a P&S super zoom
digital camera versus a DSLR. The DSLR image has less noise and
more detail. The DSLR used a 300 mm f/4 lens with image stabilization
and was hand held. Noise in the P&S image hides and confuses
much of the fine detail, and diffraction and lens
quality limits actual detail. Note also the sharpness of the
edge of the Moon in the upper right corner.
The contrast in the P&S image is also lower, partly because
fine detail is near the diffraction limit where the Modulation
Transfer Function (MTF, a measure of contrast), is very low.
Both images were obtained at ISO 200. The FZ35 image was make at the
longest focal length of the zoom (86.4 mm), f/6.3, 1/320 second.
The DSLR was 1/500 second at f/8, produced from the raw file.
If we had perfect lenses, diffraction and pixel sampling in a digital camera still limits the detail we could get on a subject. In Figures 5a and 5b we show we show the combined effects of diffraction and pixel size for several camera and lens combinations as we add teleconverters. If a line starts at f/4, then the point at f/5.6 is the f/4 lens plus a 1.4x teleconverter, f/8 is the f/4 lens plus a 2x teleconverter, f/11 is the f/4 lens + stacked 1.4 and 2x teleconverters, and f/16 is stacked 2x teleconverters. Trend lines that start at f/2.8 are for f/2.8 lenses, then at f/4 would be the lens + 1.4x Teleconverter, f/5.6 the lens + 2x teleconverter, and so on. Image quality of supertelephotos is still excellent with stacked teleconverters as shown in Figure 3.
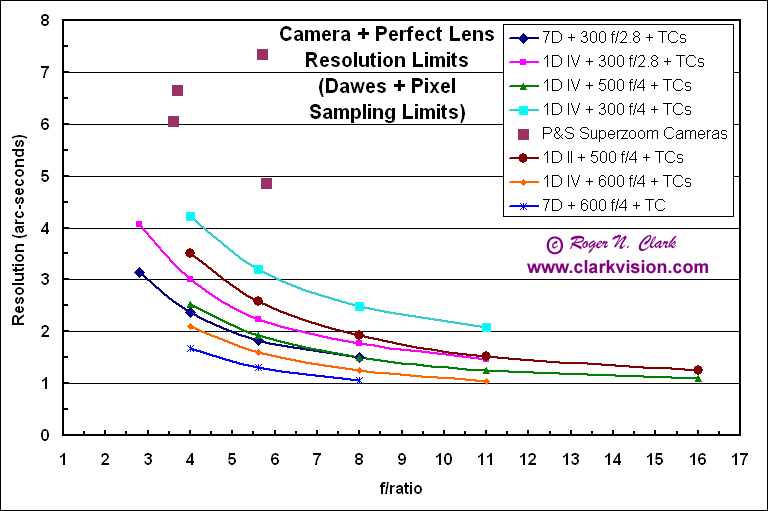
Figure 5a. Resolution computed as a combination of the Dawes limit
due to diffraction and the pixel sampling for various cameras.
A lower value means better resolution and more detail on a subject.
The trend in a single lens with increasing f/ratios due to adding
teleconverters and NOT by stopping the lens aperture down.
The trend extends beyond where a typical lens + teleconverter
will autofocus (one could use live view to focus).
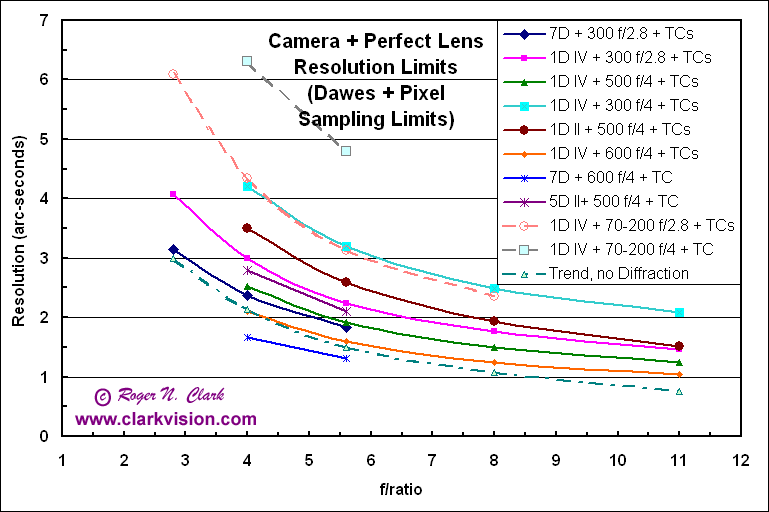
Figure 5b. Same as in Figure 4a: Resolution computed as a
combination of the Dawes limit
due to diffraction and the pixel sampling for various cameras.
A lower value means better resolution and more detail on a subject.
The trend in a single lens with increasing f/ratios due to adding
teleconverters and NOT by stopping the lens aperture down.
Also shown is a trend line if there were no diffraction.
The trend line shows the trend due to adding teleconverters
with no diffraction. The trends of actual lenses
have shallower slopes due to the effects of diffraction.
In this plot, the trend lines end where a particular lens +
teleconverter will no longer autofocus.
The trend lines in Figures 5a and 5B are for perfect lenses. In actual practice, the blur filter in digital cameras will push the curves higher. Lens aberrations will also push the curves higher, and in general, zoom lenses will have more aberrations than fixed focal length lenses.
The trend lines show, that for available telephoto lenses, resolving details finer than about 1 arc-second is very difficult. To resolve finer details, larger apertures are needed. The current largest aperture lens in the Canon lineup is the 600 mm focal length, f/4, (aperture = 150 mm). A 150 mm aperture has a Dawes diffraction limit of 0.77 arc-seconds (green light). The large pixels in current DSLRs reduce that resolution to around an arc-second or a little larger.
For reference, an animal at 50 meters distance, one arc-second is about 1/4 mm, which might be the size of a very thick hair or whisker.

Figure 6. Comparison of three 300 mm lenses: a 300 mm f/2.8,
a 300 mm f/4, and a 70-300 mm zoom at 300 mm f/5.6. Note that
as one adds TCs, diffraction becomes a greater impact on the
performance of the smaller lenses. The 420 mm line represents
the 300 mm lens with a 1.4x TC, the 600 mm line a 2x TC, and the
840 mm line stacked 2 + 1.4x TCs. Note that on consumer DSLRs, autofocus
is lost for configurations slower than f/5.6. Figure 2 illustrates that
the 300 f/2.8 lens still produces very sharp images with stacked
2 + 1.4x teleconverters.
The diffraction effects at a constant focal length and different apertures is illustrated in Figure 6 where three different 300 mm telephoto lenses are shown. As teleconverters are added, diffraction effects become a greater factor in resolving fine detail. The smaller aperture lenses lose detail to diffraction to a greater extent than the larger aperture lenses. Not considered in Figure 6: the zoom lens is likely not as sharp due to other aberrations so the curve for a real lens is likely higher on the graph, giving lower resolution.
The bottom line is that for well made lenses, larger apertures reduce the effects of diffraction, providing greater fine detail in images, not to mention faster f/ratios that enable faster shutter speeds and shallower depth-of field to isolate a subject.
Next we explore the different super telephoto lenses available on some DSLRs. The resulting resolution and difference between different lenses depends on the pixel sampling. Again, these calculations assume the lenses are diffraction limited with teleconverters attached. My experience is that super telephoto lenses are close to diffraction limited when matched lens and teleconverters from the same manufacturer are used.
Results for the Canon 1D Mark IV (5.7 micron pixel pitch) is shown in Figure 7a. The graphs show that there are modest gains as one moves up in the lens series. This is due to diffraction limiting resolution and pixel sampling limiting resolution further. For example, the 600 f/4 lens has an aperture of 150 mm, and the 400 f2.8 lens has an aperture of 143 mm, thus the limits from diffraction are similar. The 500 f/4 lens has an aperture of 125 mm, and we see in Figure 7a that the resolution is slightly worse, as expected due to diffraction effects of the different sized apertures.
The results for the Canon 7D (4.3 micron pixel pitch) tells a different story (Figure 7b). There is little difference between the high end telephotos (500 mm f/4, 600 mm f/4, and 400 mm f/2.8) because diffraction is limiting the detail and the smaller pixel sampling is hitting that limit. If you compare the 7D resolution at the same f/ratio as those for the 1D Mark IV in Figure 7a, you will see that the 7D resolution is about the same even though the 7D has finer pixel pitch. Again, this is due to limits imposed by diffraction.
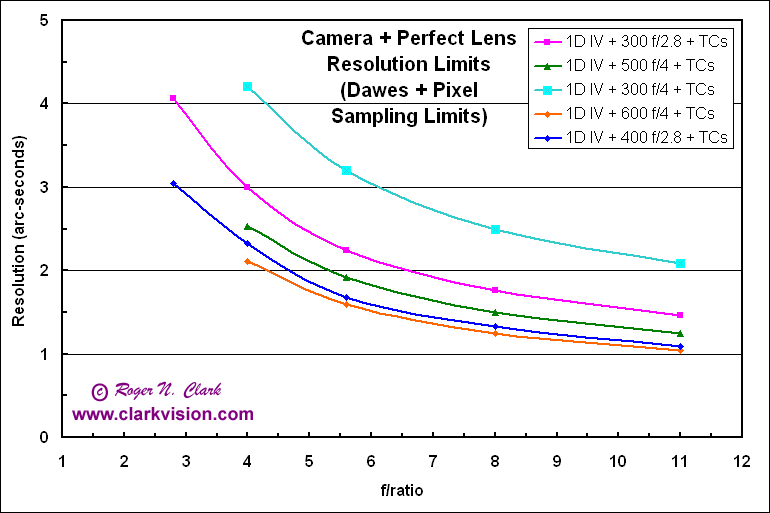
Figure 7a. Resolution for the Canon 1D Mark IV and various telephoto lenses.
The 1D series cameras will autofocus at f/8. One can stack teleconverters
at reach a longer focal length at f/11 because only one teleconverter
reports to the camera.
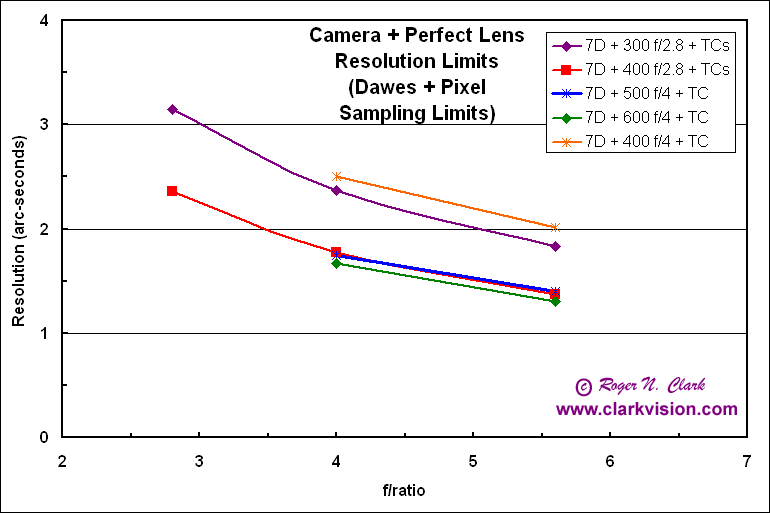
Figure 7b. Resolution for the Canon 7D and various telephoto lenses.
The smaller pixel sampling of the 7D (4.3 microns) shows that the
resolution is similar in the top telephoto lenses. This is because
the aperture diameter is similar with these lenses. The Canon 800 mm
f/5.6 plots between the 600 mm f/4 and the 400 mm f/2.8. No data
are shown beyond f/5.6 because the 7D loses autofocus.
In the discussion so far, the limiting resolution was presented. But as sampling approaches that limit, contrast drops in the fine details in an image. Figure 8 shows the contrast as a function of pixel pitch for different f/ratios. One can determine the image degradation before the resolution limit is reached. For example, the 1D Mark IV has 5.7 micron pixels, and when using an f/4 lens, the MTF is between 40 and 50% (depends on color), which means the pixel to pixel contrast is reduced to 40 to 50% of the true value. At f/8, it gets reduced to about 10%. This illustrates that diffraction mainly reduces contrast. We perceive the degradation on sharpness in an image when the detail is below the resolution limit (the Dawes limit is within a couple of percent of the 0% contrast resolution limit).

Figure 8. Diffraction affects image detail by reducing contrast. The technical
term for the contrast reduction is called the Modulation Transfer Function (MTF)
and describes the contrast the camera delivers as a function of the spacing of lines (called
the spatial frequency). Here the spatial frequency is expressed in terms
of pixel spacing. As the f/stop increases, the diffraction spot becomes larger,
and fine detail in the image becomes reduced in contrast. The red, green
and blue lines show the diffraction effects for red, green and blue wavelengths
of light for f/ratios 1, 2, 4, and 8.
A real workd demonstration of diffraction degrading contrast and image quality is shown in Figure 9. Image quality is similar from f/2.8 to f/8, with a slight peak in quality at f/5.6. But beyond f/8, contrast and image quality steadily drops as the aperture is closed. At f/5.6, the aperture of this lens is 53.6 mm (300/5.6). The measured contrast (MTF) for this series is shown in Figure 10.

Figure 9. A test target as a function of f/ratio for the very sharp
300 f/2.8 L IS lens and the Canon 7D camera which has a sensor
with 4.3 micron pixels. Peak sharpness is at f/5.6. Faster f/ratios
include other aberrations that limit image detail. F/ratios slower
than f/8 (larger numbers to the right) degrade image quality
due to diffraction.
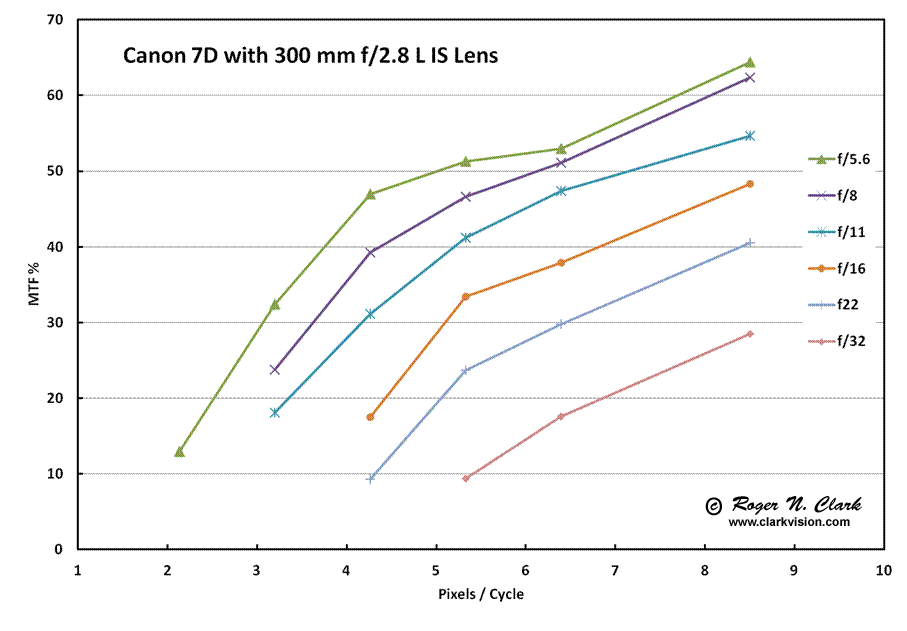
Figure 10. Modulation transfer Function (MTF), or contrast, for different
f/ratios is shown. Contrast and image quality steadily decreases as
the aperture is closed from f/5.6 to f/32 due to increasing diffraction.
Discussion
The controlling factor in telephoto reach is "pixels on subject," but is limited by diffraction. Pixels on subject is controlled by 2 variables: real focal length, and pixel pitch, assuming the lens can deliver the detail. Lens limiting detail is diffraction and aberrations. Diffraction limits are inversely proportional to lens aperture.
If you know the size of your subject, you can compute the size in pixels:
Subject size in pixels = size in arc-seconds / plate scale.
The Moon, for example, is about 1800 arc-seconds in diameter, so it would appear 1800 / 1.8 = 1000 pixels in diameter in 5D Mark II and 30D images with a 700 mm lens.
If you know the size of a subject and its distance, you can compute its apparent size
in arc-seconds:
subject angular size = 206265 * subject size / subject distance.
If you know the distance, you can compute the size of one pixel. For
example, if the Moon was 240,000 miles away, then the size of one pixel
is:
linear size of one pixel = distance*((pixel size in microns)/1000)/(focal length in mm)
For the Moon at 240,000 miles, images with a 700 mm lens using a camera with
5.7 microns pixels, one pixel would be:
size = 240000 miles * (5.7 microns/1000 microns/mm)/(700 mm) = 1.95 miles.
The above results show how difficult it would be to resolve one of the lunar landers from the Apollo missions left on the Moon.
Another example: a 0.5 meter tall bird at 50 meters appears: 206265 * 0.5 / 50 = 2063 arc-seconds across, about the size of the Moon. The Canon 30D with a 700 mm lens would make an image of the bird 2063 / 1.8 = 1146 pixels, and one pixel would be 50 meters *.0057/700 = 0.0004 meters = 0.4 mm.
Conclusions
Making sharp images with telephoto lenses and getting as much detail as possible on a subject requires a quality, large aperture lens, but how much detail one gets is also a function of the lens focal length, and the pixel pitch of the digital camera. Zoom lenses are not as sharp as fixed focal length lenses at long telephoto ranges, especially consumer zoom lenses.
Next:
Telephoto Reach, Part 2: Telephoto + Camera System Performance
(A Omega Product, or Etendue, Advanced Concepts)
Additional Reading
Crop Factor and Digital Cameras
Pixel Size, ISO and Noise in Digital Cameras
Digital Cameras: Does Pixel Size Matter?
Factors in Choosing a Digital Camera (Does Sensor Size Matter?)
Good digital cameras are photon noise limited. This sets basic properties
of sensor performance.
The f/ratio Myth and Digital Cameras.
Etendue, or Optical Throughput.
| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
http://clarkvision.com/articles/telephoto_reach
First Published October 31, 2010
Last updated March 11, 2012.