| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
by Roger N. Clark
This review shows an analysis of noise, dynamic range, and full well capacity of a Canon 1D Mark II digital camera. It also shows the dark current and noise from thermal dark current as a function of temperature.
How well do digital cameras perform? On this web page, I'll show the details on how to evaluate the sensor in a digital camera. Using simple models one can test various possible noise sources in a camera system. The lowest possible noise from a system detecting light is the noise due to Poisson statistics from the random rate of arrival of photons. This is called photon statistics, or photon noise. Noise from the electronics will add to the photon noise. We will see that the Canon 1D Mark II is limited by photon statistics at high signal levels and by electronic noise from reading the sensor (called readout noise) at very low signal levels. In the case of high signal levels, a system that is photon statistics limited enables us to directly measure how many photons the sensor captures, and by increasing the exposure, we can determine how many photons are required to saturate the sensor. That is called the full well capacity.
In order to analyze a camera, one needs appropriate data. This is very simply done. Here are the steps.
The challenge in analyzing noise and full well capacities of a camera sensor is obtaining data that is free of artifacts. Artifacts could include non-uniformity of the light field (e.g. due to vignetting in the lens), dust specs on the sensor, pixel to pixel sensitivity variations and other effects. Fortunately, there is a simple way to neutralize these effects. If you take pairs of images at the same exposure and in rapid succession, then difference the two images, the residuals for a quality sensor is the noise due to electronics plus photons. Light variations are eliminated. But one should try and make a uniform setup in order to drive all pixels at very close to the same light level.
Experiment Setup
I chose a uniformly lit wall in a room with mostly white walls. I chose a room with multiple lights plus sunlight coming in through a window. I put a 180mm f/3.5 lens on the camera and mounted it on a tripod. I focused the lens to infinity and placed the lens about a half meter from the wall. This setup ensures the wall is out of focus, and that a small portion of the wall is in the field, so a reasonably uniform signal illuminates the sensor.
Obtaining the Data Set
Set the camera to its lowest ISO setting. I first metered the scene to see what a good exposure would be. I then set the camera on manual and took a series of exposures in pairs. Exposures ranges from the minimum the camera was capable of, to a long enough exposure that all pixels were saturated in all colors. The exposures I used ranged from 1/8000 second to 0.8 second and I used two f/stops (f/5.0 and f/5.6). There is no need to vary the f/stop, but if you do you can check the accuracy of the f/stops too. At each exposure setting, two images are obtained within a few seconds of each other. I waited for the data to be written to the memory card before doing the next exposure. I did exposures pairs at both the lowest ISO setting, and at a high setting, in this case ISO 1600. Only the ISO 50 data are presented here.
A second set of data tests read noise. Put the lens cap on the camera and set the exposure time to the maximum the camera will do (1/8000 second for the 1D Mark II). For each ISO setting, take a pair of exposures. I did ISO 50, 100, 200, 400, 800, 1600, and 3200.
Here is a more complete write-up on taking the data: How to Take the Data .
Data Processing
The procedure below is based on using ImagesPlus 2.5, hereafter called IP. The image processing system you use must be able to convert the raw data with a linear scale (Photoshop will not do this) and process the data with at least 16-bit math (IP uses 64-bit floating point math).
Results
Results for determining read noise is shown in Table 1a. Column B is the standard deviation from subtracting two images, and Column C = column B / 1.4142. Column D = column C / 16 which scale the 16-bit DNs to camera 12-bit DNs. Column E is the gain derived from data in Table 2 by dividing the high signal in electrons by camera DN. Gains at ISOs higher than 50 are scaled relative to that at ISO 50 (this scaling agrees within the noise of determining gains at each ISO). Read noise, Column F = Column D * Column E. Dynamic range, Column G = maximum signal / read noise. Maximum signal is 79,900 electrons (Table 2) at ISO 50, and 53,000 electrons at ISO 100. Higher ISO reduces the maximum electrons relative to ISO 100 (e.g. ISO 200 is half the electrons of ISO 100). Column H is the square root of the number of photons recorded (e.g. square root 79,900 at ISO 50; square root 53,000 at ISO 100).
| A | B | C | D | E | F | G | H |
| ISO |
2-image 16-bit Std Dev DN | 16-bit Std Dev per pixel (DN) | Camera noise Std Dev (12-bit DN) | Camera Gain (12-bit) (electrons/DN) |
Read Noise (electrons) |
Dynamic Range |
Maximum Signal-to-Noise ratio |
| 50 | 26.618 | 18.822 | 1.176 | 26.03 | 30.62 | 2610 | 283 |
| 100 | 28.871 | 20.415 | 1.276 | 13.02 | 16.61 | 3190 | 230 |
| 200 | 31.104 | 21.994 | 1.375 | 6.51 | 8.95 | 2960 | 163 |
| 400 | 38.686 | 27.355 | 1.710 | 3.25 | 5.56 | 2380 | 115 |
| 800 | 56.219 | 39.753 | 2.485 | 1.63 | 4.04 | 1640 | 81 |
| 1600 | 108.604 | 76.795 | 4.800 | 0.81 | 3.90 | 850 | 58 |
| 3200 | 218.527 | 154.522 | 9.658 | 0.41 | 3.93 | 420 | 41 |
Using data from the analysis here, the sensor performance is summarized in Figure 1b. The gain (Table 1b, column B) reaches unity at about ISO 1300. Once gain drops below 1 electron/DN, there is little point in increasing ISO further. The effect of higher ISO above unity gain only decreases dynamic range without helping to detect lower signals.
Table 1b: Canon 1D Mark II: Derived Sensor Performance
A B C D E F G
Camera Apparent
ISO Gain Read Noise Maximum Dynamic Dynamic Maximum
(electrons/ (electrons) Signal Range Range Signal-to-Noise
12-bit DN) (electrons) (linear) (stops) Ratio
50 26.03 30.62 79,900 2,610 11.3 283
100 13.02 16.61 53,000 3,190 11.6 230
200 6.51 8.95 26,500 2,960 11.5 163
400 3.25 5.56 13,200 2,380 11.2 115
800 1.63 4.04 6,620 1,640 10.7 81
1600 0.81 3.90 3,310 850 9.7 58
3200 0.41 3.93 1,650 420 8.7 41
The camera noise statistics are shown in Table 2. The normalized exposure time, Column B, normalizes the changes in f/stops used during the test (f/5.0 and f/5.6). The average DN, Column C, is the average signal observed in a 200 x 200 pixel patch in the center of the image. A model was constructed to check system linearity, Columns D and E. The model in Column D = (3354.27 * Column B/0.4)-7. The constant 3354.27 is the average signal for image JZ3F7540, and the constant 7 represents an offset in the electronics to keep the signal level above 0. The constant 0.4 scales the exposure time relative to that of the reference image, JZ3F7540. The system linearity, Column E = Column C / Column D, and is within a few percent, which is very good. System linearity includes the detector linearity, shutter reproducibility, f/stop reproducibility, and light source stability. Note in the shorter shutter speeds, the signal level in pairs of exposures varies a small amount. This was traced post experiment to a nearby fluorescent light that contributed a high frequency flicker to the light signal. That light is at least partly responsible for the variable signal levels at a few percent level in short exposures. That would not effect noise determinations, however. The lesson is check all light sources and be sure only incandescent lights contribute to the signal.
Pairs of the same exposure time and f/stop were subtracted and the standard deviation divided by square root 2 is shown in Column F of Table 2. The signal-to-noise ratio, Column G, is the values in Column F divided by those in Column C. If the sensor is photon noise limited, the trend in this ratio is a square root dependence. There are several ways to determine the number of converted photons (the number of electrons) from the sensor. A common way is to evaluate sensor noise is to plot the variance versus signal (References 1, 3). That is a straight line if the system is photon noise limited and the slope of the trend represents the gain in electrons/DN, and similar a trend line is shown in Figure 3 from data in Column I. While both methods are equally valid, I prefer analyzing the signal-to-noise ratio because that ratio squared directly equals the number of photons collected without needing gain conversions, or computing the slope of a line.
So, is the Canon 1D Mark II photon noise limited? Column H shows a model that uses the read noise from Table 1 (30.62 electrons at ISO 50) and the Signal to noise ratio derived from the model from Table 2, Column D and the system gain. The equation is:
H = (D*26.03/16)/(sqrt(D*26.03/16 + 30.62*30.62)), (eqn 1)
where the letters H and D are the values in Columns H and D in Table 2. The value 16 scales 16-bit Column D DNs to Camera 12-bit DN to match the units of the gain, 26.03 electrons/12-bit camera DN.
The Canon 1D Mark II signal-to-noise ratio data and model (Columns G and H in Table 2) are plotted in Figure 2. The fact that the model matches the data very well indicates there are no other sources of noise contributing to the data at any significant level. Thus, for high signal levels, the 1D Mark II is photon noise limited. This means further improvements in electronics will not improve the signal-to-noise ratio for high signal levels. If the quantum efficiency were improved with a different sensor, that would certainly improve the signal-to-noise ratio.
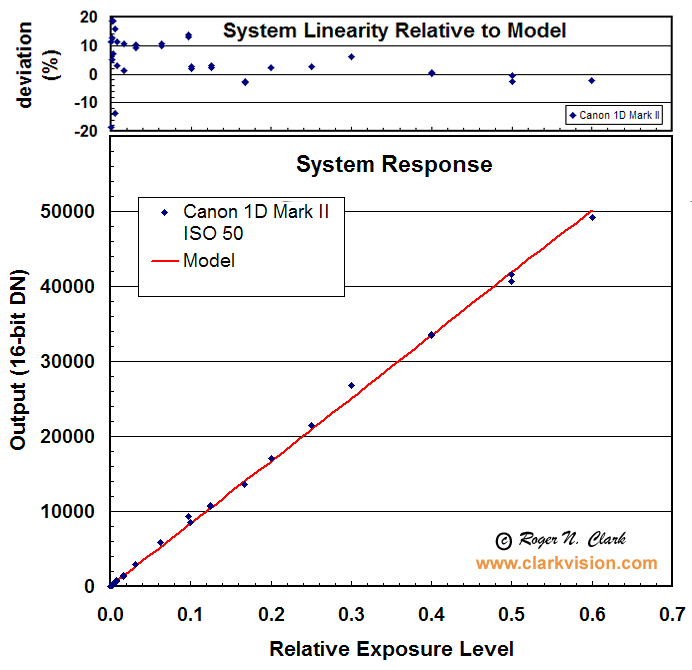
Figure 1. The Canon 1D Mark II shows a very linear trend with signal.
Variations in signal level include repeatability of the shutter and aperture,
as well as the light source.
The model is the average DN from image JZ3F7540 scaled according to exposure
time and subtract 7 DN.
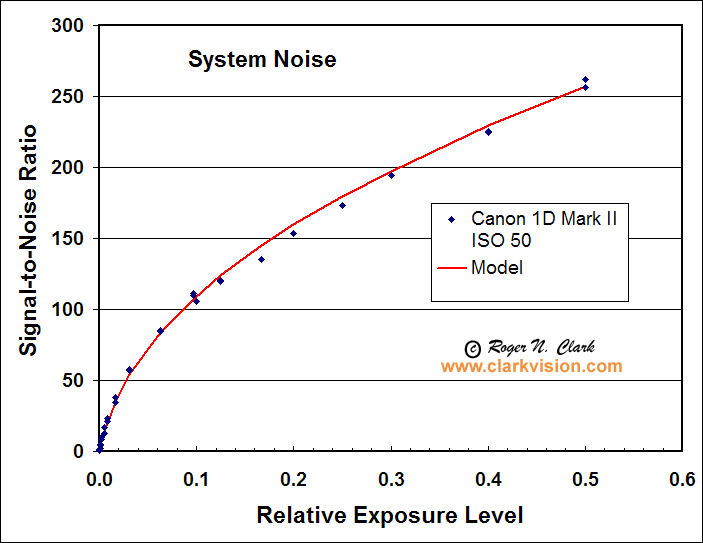
Figure 2. Signal-to-noise ratio observed and predicted. The prediction
model uses photon statistics and read noise.
Model is average DN scaled to electrons plus read noise. For this case,
ISO 50, the gain is 26.03 electrons/DN, and the read noise is 30.62 electrons.
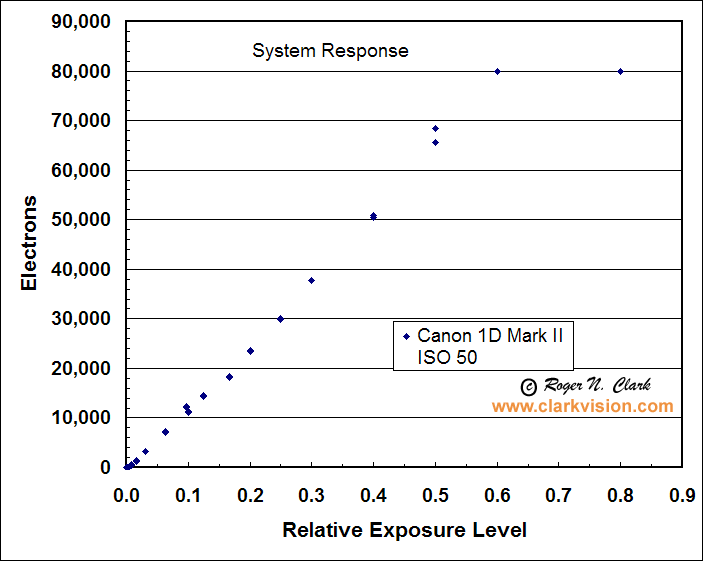
Figure 3. The electrons converted by the canon 1D Mark II sensor
are shown relative to exposure level. The sensor saturates at about
79,900 electrons, but is quite linear below that level.
Noise Sources
The "read noise" in Tables 1a and 1b vary with ISO and have been a source of confusion to phtographers reading these results. The analog-to-digital converter (A/D, or ADC) used in the Canon 1D Mark II is 12-bits. Noise specifications for typical 12-bit A/Ds running in the tens of megahertz range are expressed in decibels (dB) and typically give about a 70 dB signal-to-noise ratio. Twelve bits if perfect would give 72.2 dB (=20 log(4095)), so 70 dB is very good. In Figure 4, the noise floor is modeled as a function of ISO, using the data in Table 1a. Only 2 noise sources are needed to model the observed noise: a base level of sensor read noise that is constant at all ISOs, and a constant 70.5 dB of noise-to-noise ratio from the A/D converter. This illustrates that newer cameras employing 14-bit converters should have improved performance at low ISO. The Figure also illustrates one should use ISOs of 800 or higher for low light work, because the noise is dominated only by sensor read noise.
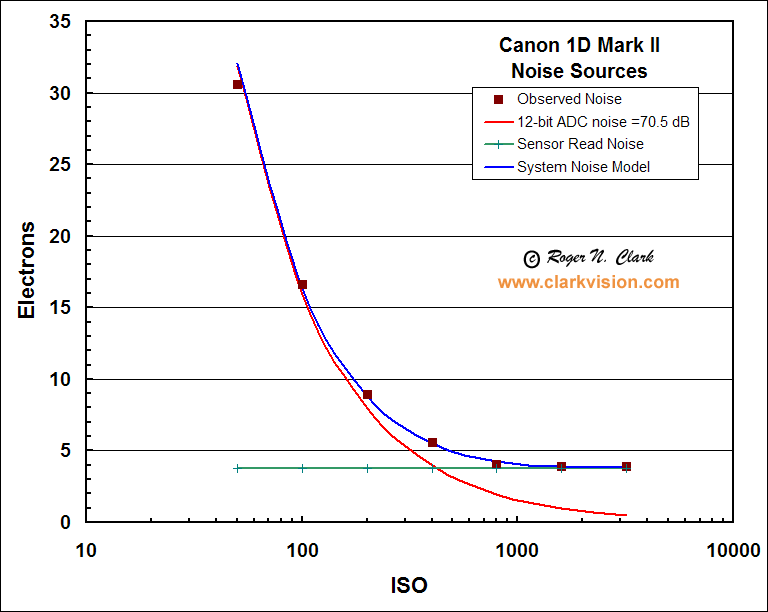
Figure 4. Camera noise sources for fast shutter speeds
are well modeled with only two sources: sensor read noise and
noise from the analog-to-digital converter.
The noise model is the square root of the sum of the squared
noise sources (A/D signal-to-noise ratio = 70.5 dB
and the sensor read noise =3.8 electrons).
The observed noise are the values from Table 1a, column F.
Dark Current and Related Noise
Another noise component is due to dark current, which will increase with exposure time. Dark current and its noise is also a function of the temperature of the sensor and associated electronics.
Dark current was measured at room temperature for 623 and 1800 second exposures at ISO 1600. Pairs of images were analyzed similar to that done for read noise. There is not a clean answer because as exposure time increases, dark current for each pixel is obviously quite variable, resulting a large variation in signal. Long exposure images look like they have a lot of noise spikes. Average dark currents were measured at 0.013 to 0.02 electrons/second, but some pixels have dark currents as high as about 0.25 electrons/second. In an 1800 second exposure, that translates to signal levels of 23 to 450 electrons, and noise of 5 to 21 electrons. It is this pixel to pixel variation that limits the image quality of long exposures (Figure 4).
Figure 4. The noise in a 1D Mark II image is shown in this cropped
portion at full scale (1 camera pixel to 1 image pixel) for an
1800 second exposure at ISO 1600. Linear raw conversion in ImagesPlus 2.5.
Figure 5. A 623 second exposure of a target illuminated by only
0.00016 lux. The 1D Mark II camera was operating at room temperature
and ISO 1600 with a 50mm f/1.8 lens. This image has had no stretching
or processing other than raw image conversion in photoshop
with default settings, then the two rows cropped
from the full image and downsampled about 4x.
The width of the image is the full height of the original image.
The tilt of the target was intentional so image edges did not line up
with rows of pixels.
A test of a long exposure is shown in Figure 5. The 623 second exposure at ISO 1600 shows some noise but is generally a very good image considering the illumination was only 0.00016 lux (similar to an overcast night away from cities with no moon; it took several minutes of dark adaption to to begin to see the target in the room). The light detected is shown in Table 3 along with the noise analysis and model prediction.
| Color Chart Patch |
Average Intensity (Photons) | Photon Rate (Photons per pixel/second) | Measured Noise (electrons) | Noise Model (electrons) |
| A | 749.4 | 1.21 | 26.9 | 30.3 |
| B | 494.9 | 0.794 | 24.0 | 25.8 |
| C | 288.7 | 0.463 | 22.7 | 21.4 |
| D | 148.5 | 0.238 | 21.4 | 17.9 |
| E | 60.6 | 0.097 | 21.2 | 15.2 |
| F | 19.4 | 0.031 | 16.8 | 13.8 |
The data in Table 3 shows that DSLRs like the 1D Mark II can operate at very low light levels at room temperature. The noise model is:
N = (P + r2 + t2)1/2, (eqn 2)
Where N = total noise in electrons, P = number of photons, r = read noise in electrons, and t = thermal noise in electrons. Noise from a stream of photons, the light we all see and image with our cameras, is the square root of the number of photons, so that is why the P in equation 2 is not squared (sqrt(P)2 = P). The model used the read noise of 3.9 electrons from Table 1. The thermal noise squared = the dark current = 0.25 electrons/second * 623 seconds = 157.75 electrons2. Similar noise models are discussed in reference 6.
Pattern noise in long exposure dark frames is shown in Tables 4a, 4b and 4c.
| Table 4a. Thermal Noise, Central Image | |
 |
ISO 1600 Exposure= 623 seconds T= 20 C Image Range: -100.00 to 100.00 electrons about the mean Central 500 x 300 pixel statistics: min= 21 electrons max= 3006 electrons mean= 104 electrons standard deviation= 48.77 electrons |
| Table 4b. Thermal Noise, Full Image, sub-sampled | |
 |
ISO 1600 Exposure= 623 seconds T= 20 C Image Range: -100.00 to 100.00 electrons about the mean Full image statistics: min= 6 electrons max= 3006 electrons mean= 106 electrons standard deviation= 50.76 electrons |
| Table 4c. Thermal Noise, Full Image, sub-sampled | |
 |
ISO 1600 Exposure= 623 seconds T= 20 C Image Range: -20.00 to 20.00 electrons about the mean Full image statistics: min= 6 electrons max= 3006 electrons mean= 106 electrons standard deviation= 50.76 electrons |
Conclusions
The data shown here for the Canon 1D Mark II shows that the camera is operating and near perfect levels for the sensor. This means that for high signals, noise is dominated by photon statistics. Noise at low signal levels can be improved, but is very good. To achieve higher signal-to-noise ratio images, a higher quantum efficiency sensor with a larger full well would be needed. Without increasing the full well capacity, the maximum signal-to-noise ratio would not improve, but that the signal-to-noise ratio at ISO 50 could be achieved at higher ISOs if the quantum efficiency were improved. Improvements in quantum efficiency of 3 to 4x are possible (Reference 2).
The data for the 1D mark II indicate some important aspects for people making images. The lowest ISO, 50, does have higher signal-to-noise ratios than ISO 100, but at the expense of lower dynamic range and danger of saturating highlights. An ISO of about 75 would be a better match to the sensor range and would not sacrifice dynamic range. Unfortunately, ISO 75 is not available.
For low light imaging, high ISO will record fainter light. There is no advantage in using ISO 3200 and in fact there is a disadvantage in reduced dynamic range. ISO 1600 is the optimum with the lowest read noise, but ISO 800 is almost as good (almost the same read noise as ISO 1600) with the advantage of almost double the dynamic range of ISO 1600. Long exposures suffer from dark current that varies over a factor of ten from pixel to pixel, ultimately limiting image quality of long exposures. If dark current could be made more uniform, much longer exposures could be made with high image quality. Even so, 10+ minute exposures at ISO 1600 still produce acceptable images, recording only a few photons.
With the details of how to evaluate sensor noise presented here, everyone can evaluate their own cameras. For other descriptions, see References 1 and 3.
References
1) CCD Gain. http://spiff.rit.edu/classes/phys559/lectures/gain/gain.html
4) http://www.photomet.com/library_enc_fwcapacity.shtml
7) dcraw. http://www.cybercom.net/%7Edcoffin/dcraw 8) dcraw manual page. 9) dcraw downloads.
Notes:
DN is "Data Number." That is the number in the file for each pixel. I'm quoting the luminance level (although red, green and blue are almost the same in the cases I cited).
16-bit signed integer: -32768 to +32767
16-bit unsigned integer: 0 to 65535
Photoshop uses signed integers, but the 16-bit tiff is unsigned integer (correctly read by ImagesPlus).
| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
http://www.clarkvision.com/reviews/evaluation-1d2
First published July 8, 2007.
Last updated January 18, 2014