
Canon 1D Mark II Review and Sensor Analysis
Plus Procedures for Evaluating Digital Camera
Sensor Noise, Thermal Noise, Dynamic Range, and Full Well Capacities
by Roger N. Clark
This review shows an analysis of noise, dynamic range, and full well capacity
of a Canon 1D Mark II digital camera.
It also shows the dark current and noise from thermal
dark current as a function of temperature.
All images, text and data on this site are copyrighted.
They may not be used except by written permission from Roger N. Clark.
All rights reserved.
If you find the information on this site useful,
please support Clarkvision and make a donation (link below).
How well do digital cameras perform? On this web page, I'll
show the details on how to evaluate the sensor in a digital camera.
Using simple models one can test various possible noise
sources in a camera system. The lowest possible noise from a
system detecting light is the noise due to Poisson statistics
from the random rate of arrival of photons. This is called
photon statistics, or photon noise. Noise from the electronics
will add to the photon noise. We will see that
the Canon 1D Mark II is limited by photon statistics at high
signal levels and by electronic noise from reading the sensor
(called readout noise) at very low signal levels.
In the case of high signal levels, a system that is photon statistics
limited enables us to directly measure how many photons
the sensor captures, and by increasing the exposure, we can
determine how many photons are required to saturate the
sensor. That is called the full well capacity.
In order to analyze a camera, one needs appropriate data. This is
very simply done. Here are the steps.
The challenge in analyzing noise and full well capacities of a
camera sensor is obtaining data that is free of artifacts.
Artifacts could include non-uniformity of the light field
(e.g. due to vignetting in the lens), dust specs on the sensor,
pixel to pixel sensitivity variations and other effects.
Fortunately, there is a simple way to neutralize these effects.
If you take pairs of images at the same exposure and in rapid
succession, then difference the two images, the residuals
for a quality sensor is the noise due to electronics plus
photons. Light variations are eliminated. But one should
try and make a uniform setup in order to drive all pixels
at very close to the same light level.
Experiment Setup
I chose a uniformly lit wall in a room with mostly white
walls. I chose a room with multiple lights plus sunlight coming
in through a window. I put a 180mm f/3.5 lens on the camera
and mounted it on a tripod. I focused the lens to
infinity and placed the lens about a half meter from the
wall. This setup ensures the wall is out of focus,
and that a small portion of the wall is in the field, so
a reasonably uniform signal illuminates the sensor.
Obtaining the Data Set
Set the camera to its lowest ISO setting.
I first metered the scene
to see what a good exposure would be. I then
set the camera on manual and took a series of
exposures in pairs. Exposures ranges from the
minimum the camera was capable of, to a long
enough exposure that all pixels were saturated
in all colors. The exposures I used ranged
from 1/8000 second to 0.8 second and I used
two f/stops (f/5.0 and f/5.6). There is no
need to vary the f/stop, but if you do you
can check the accuracy of the f/stops too.
At each exposure setting, two images are obtained
within a few seconds of each other. I waited
for the data to be written to the memory card
before doing the next exposure.
I did exposures pairs at both the lowest ISO setting,
and at a high setting, in this case ISO 1600.
Only the ISO 50 data are presented here.
A second set of data tests read noise. Put the lens
cap on the camera and set the exposure time
to the maximum the camera will do (1/8000 second
for the 1D Mark II). For each ISO setting,
take a pair of exposures. I did ISO 50,
100, 200, 400, 800, 1600, and 3200.
Here is a more complete write-up on taking the data:
How to Take the Data .
Data Processing
The procedure below is based on using ImagesPlus 2.5,
hereafter called IP. The image
processing system you use must be able to convert the raw
data with a linear scale (Photoshop will not do this) and
process the data with at least 16-bit math (IP
uses 64-bit floating point math).
- Raw conversion: convert with no white balance, select CFA.
Save the images in either 16-bit tiff or compressed FIT
(I use lossless compressed FIT as it saves a lot of disk space).
An excellent raw converter (free) is dcraw. Convert the
raw files with: dcraw -D -4 -j -t 0 -T rawfilename and this
makes a tif file.
- Split the Bayer CFA (this is under the color menu).
I open all images in IP, then open the split Bayer CFA
window. Select each image, click apply and the red, green
and blue images will be created. Click on each image,
and save (confirm the over-write or the image will go away
later), then close each one after saving.
- I move the red, green, and blue images to their own
subdirectories for processing.
- Next, cd to the green directory, and crop the files.
I crop about the center (default) with width and height
of 200 pixels each. This is done as one step in IP
under files, image file operations, crop files.
- Open a pair of cropped images done at the same exposure.
Also open the cross hair statistics tool. The tool gives
the average intensity and standard deviation for the entire image.
Record the average intensity for each image.
- Now subtract the the two images with the image math
tool (under the point menu). To do this, open the
image math tool, then click the select source 1 box,
then click on one of the two images, then select
the other source box and click on the other image.
The images are 16-bit unsigned integers, so you must
do a trick to make sure the subtraction does not go
below zero. Under source 2, type in an offset
of 1000 or 2000, or more. The value does not matter,
except you want to be sure that the subtraction does
not go below zero. Click the subtract button and
the subtracted image is created. The cross hair
statistics tool will show the standard deviation,
minimum and other statistics. Be sure the minimum
is above zero. If not, increase the offset and
click subtract again in the image math window.
The standard deviation represents the noise in
TWO images. The noise in one image is square
root 2 less, so divide the standard deviation
by root 2 (1.4142) and record that value for both
images.
Results
Results for determining read noise is shown in Table 1a. Column B is the standard
deviation from subtracting two images, and Column C = column B / 1.4142.
Column D = column C / 16 which scale the 16-bit DNs to camera 12-bit DNs.
Column E is the gain derived from data in Table 2 by dividing the high signal in
electrons by camera DN. Gains at ISOs higher than 50 are scaled relative
to that at ISO 50 (this scaling agrees within the noise of determining gains
at each ISO). Read noise, Column F = Column D * Column E.
Dynamic range, Column G = maximum signal / read noise. Maximum signal
is 79,900 electrons (Table 2) at ISO 50, and 53,000 electrons at ISO 100.
Higher ISO reduces the maximum electrons relative to ISO 100 (e.g. ISO 200
is half the electrons of ISO 100). Column H is the square root of the number of
photons recorded (e.g. square root 79,900 at ISO 50; square root 53,000 at
ISO 100).
Table 1a: Canon 1D Mark II Read Noise and Dynamic Range
| A | B | C | D | E | F | G | H |
| ISO |
2-image
16-bit
Std Dev
DN
| 16-bit
Std Dev
per pixel
(DN) | Camera
noise
Std Dev
(12-bit DN) | Camera
Gain
(12-bit)
(electrons/DN)
|
Read Noise
(electrons) |
Dynamic
Range |
Maximum
Signal-to-Noise
ratio |
| 50 |
26.618 | 18.822 | 1.176 | 26.03 | 30.62 |
2610 | 283
|
| 100 |
28.871 | 20.415 | 1.276 | 13.02 | 16.61 |
3190 | 230
|
| 200 |
31.104 | 21.994 | 1.375 | 6.51 | 8.95 |
2960 | 163
|
| 400 |
38.686 | 27.355 | 1.710 | 3.25 | 5.56 |
2380 | 115
|
| 800 |
56.219 | 39.753 | 2.485 | 1.63 | 4.04 |
1640 | 81
|
| 1600 |
108.604 | 76.795 | 4.800 | 0.81 | 3.90 |
850 | 58
|
| 3200 |
218.527 | 154.522 | 9.658 | 0.41 | 3.93 |
420 | 41
|
Using data from the analysis here, the sensor performance is summarized in
Figure 1b. The gain (Table 1b, column B) reaches unity at about ISO 1300.
Once gain drops below 1 electron/DN, there is little point in increasing ISO
further. The effect of higher ISO above unity gain only decreases
dynamic range without helping to detect lower signals.
Table 1b: Canon 1D Mark II: Derived Sensor Performance
A B C D E F G
Camera Apparent
ISO Gain Read Noise Maximum Dynamic Dynamic Maximum
(electrons/ (electrons) Signal Range Range Signal-to-Noise
12-bit DN) (electrons) (linear) (stops) Ratio
50 26.03 30.62 79,900 2,610 11.3 283
100 13.02 16.61 53,000 3,190 11.6 230
200 6.51 8.95 26,500 2,960 11.5 163
400 3.25 5.56 13,200 2,380 11.2 115
800 1.63 4.04 6,620 1,640 10.7 81
1600 0.81 3.90 3,310 850 9.7 58
3200 0.41 3.93 1,650 420 8.7 41
The camera noise statistics are shown in Table 2. The normalized
exposure time, Column B, normalizes the changes in f/stops used during
the test (f/5.0 and f/5.6). The average DN, Column C, is the average
signal observed in a 200 x 200 pixel patch in the center of the image.
A model was constructed to check system linearity, Columns D and E.
The model in Column D = (3354.27 * Column B/0.4)-7. The constant
3354.27 is the average signal for image JZ3F7540, and the constant 7
represents an offset in the electronics to keep the signal level above 0.
The constant 0.4 scales the exposure time relative to that of the
reference image, JZ3F7540.
The system linearity, Column E = Column C / Column D, and is within a few
percent, which is very good. System linearity includes the detector
linearity, shutter reproducibility, f/stop reproducibility, and light
source stability. Note in the shorter shutter speeds, the signal
level in pairs of exposures varies a small amount. This was traced
post experiment to a nearby fluorescent light that contributed a high
frequency flicker to the light signal. That light is at least partly
responsible for the variable signal levels at a few percent level in
short exposures. That would not effect noise determinations, however.
The lesson is check all light sources and be sure only incandescent
lights contribute to the signal.
Pairs of the same exposure time and f/stop were subtracted and the
standard deviation divided by square root 2 is shown in Column F of Table 2.
The signal-to-noise ratio, Column G, is the values in Column F divided
by those in Column C. If the sensor is photon noise limited, the trend
in this ratio is a square root dependence. There are several ways
to determine the number of converted photons (the number of electrons)
from the sensor. A common way is to evaluate sensor noise is to
plot the variance versus signal (References 1, 3).
That is a straight line if the system is photon noise limited and the
slope of the trend represents the gain in electrons/DN, and similar a trend
line is shown in Figure 3 from data in Column I. While both methods
are equally valid, I prefer analyzing the signal-to-noise ratio because
that ratio squared directly equals the number of photons collected
without needing gain conversions, or computing the slope of a line.
So, is the Canon 1D Mark II photon noise limited? Column H shows a model
that uses the read noise from Table 1 (30.62 electrons at ISO 50) and the
Signal to noise ratio derived from the model from Table 2, Column D and
the system gain. The equation is:
H = (D*26.03/16)/(sqrt(D*26.03/16 + 30.62*30.62)), (eqn 1)
where the letters H and D are the values in Columns H and D in Table 2.
The value 16 scales 16-bit Column D DNs to Camera 12-bit DN to match
the units of the gain, 26.03 electrons/12-bit camera DN.
The Canon 1D Mark II signal-to-noise ratio data and model (Columns G and H in
Table 2) are plotted in Figure 2. The fact that the model matches the data
very well indicates there are no other sources of noise contributing to
the data at any significant level. Thus, for high signal levels, the 1D Mark II
is photon noise limited. This means further improvements in electronics
will not improve the signal-to-noise ratio for high signal levels. If the quantum
efficiency were improved with a different sensor, that would certainly improve
the signal-to-noise ratio.
Table 2: Canon 1D Mark II Noise Statistics
A B C D E F G H I
Normalized Predict Linearity Noise Predicted
Exposure Average norm to DN/Predict Std dev Signal/ signal/ Signal
File Name time (sec) DN JZ3F7540 (%) (DN) noise noise (electrons)
JZ3F7568 0.000125 14.54 10.49 27.86 16.939 0.859 0.552 0.74
JZ3F7569 0.000125 16.00 10.49 34.41 16.939 0.944 0.552 0.89
JZ3F7566 0.000376 20.61 24.47 -18.75 19.597 1.052 1.274 1.11
JZ3F7567 0.000376 27.59 24.47 11.30 19.597 1.408 1.274 1.98
JZ3F7564 0.000627 47.83 45.46 4.96 23.015 2.078 2.325 4.32
JZ3F7565 0.000627 55.83 45.46 18.58 23.015 2.426 2.325 5.88
JZ3F7562 0.001254 112.05 97.91 12.62 24.491 4.575 4.810 20.93
JZ3F7563 0.001254 124.03 97.91 21.06 24.491 5.064 4.810 25.65
JZ3F7560 0.002509 218.37 202.83 7.12 25.909 8.428 9.268 71.04
JZ3F7561 0.002509 249.63 202.83 18.75 25.909 9.635 9.268 92.83
JZ3F7558 0.005018 490.64 412.65 15.90 28.527 17.199 16.737 295.81
JZ3F7559 0.005018 362.52 412.65 -13.83 28.527 12.708 16.737 161.49
JZ3F7556 0.007903 737.39 653.95 11.32 32.054 23.005 23.781 529.22
JZ3F7557 0.007903 673.15 653.95 2.85 32.054 21.001 23.781 441.02
JZ3F7554 0.016307 1518.77 1356.86 10.66 39.798 38.162 39.362 1456.33
JZ3F7555 0.016307 1371.70 1356.86 1.08 39.798 34.466 39.362 1187.94
JZ3F7552 0.031360 2914.53 2615.81 10.25 50.681 57.507 59.053 3307.07
JZ3F7553 0.031360 2880.75 2615.81 9.20 50.681 56.841 59.053 3230.86
JZ3F7550 0.062720 5867.70 5238.63 10.72 68.842 85.235 87.624 7264.93
JZ3F7551 0.062720 5826.18 5238.63 10.08 68.842 84.631 87.624 7162.48
JZ3F7527 0.100000 8530.99 8356.57 2.04 81.014 105.303 112.774 11088.67
JZ3F7528 0.100000 8585.31 8356.57 2.66 81.014 105.973 112.774 11230.33
JZ3F7548 0.096589 9361.93 8071.27 13.79 84.383 110.945 110.706 12308.86
JZ3F7549 0.096589 9277.50 8071.27 13.00 84.383 109.945 110.706 12087.85
JZ3F7529 0.125000 10701.77 10447.46 2.38 89.257 119.898 126.918 14375.50
JZ3F7530 0.125000 10765.38 10447.46 2.95 89.257 120.611 126.918 14546.90
JZ3F7531 0.167000 13553.07 13960.16 -3.00 100.351 135.056 147.686 18240.23
JZ3F7532 0.167000 13595.36 13960.16 -2.68 100.351 135.478 147.686 18354.24
JZ3F7533 0.200000 17081.52 16720.14 2.12 111.442 153.277 162.158 23493.84
JZ3F7534 0.200000 17087.82 16720.14 2.15 111.442 153.334 162.158 23511.18
JZ3F7535 0.250000 21440.86 20901.92 2.51 124.005 172.904 181.913 29895.70
JZ3F7536 0.250000 21495.32 20901.92 2.76 124.005 173.343 181.913 30047.77
JZ3F7537 0.300000 26751.08 25083.70 6.23 137.544 194.492 199.729 37827.01
JZ3F7538 0.300000 26737.60 25083.70 6.19 137.544 194.394 199.729 37788.89
JZ3F7539 0.400000 33584.17 33447.27 0.41 148.920 225.518 231.285 50858.30
JZ3F7540 0.400000 33454.27 33447.27 0.02 148.920 224.646 231.285 50465.64
JZ3F7541 0.500000 41632.24 41810.84 -0.43 159.079 261.709 259.029 68491.47
JZ3F7542 0.500000 40733.26 41810.84 -2.65 159.079 256.058 259.029 65565.48
JZ3F7543 0.600000 49136.00 50174.41 -2.11 79938.13
JZ3F7544 0.600000 49136.00 50174.41 -2.11 79938.13
JZ3F7545 0.800000 49136.00 79938.13
JZ3F7546 0.800000 49136.00 79938.13
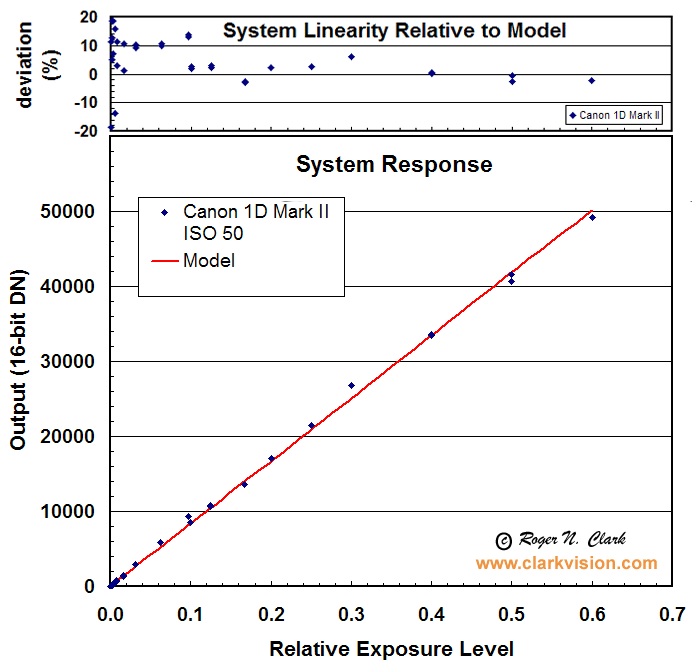
Figure 1. The Canon 1D Mark II shows a very linear trend with signal.
Variations in signal level include repeatability of the shutter and aperture,
as well as the light source.
The model is the average DN from image JZ3F7540 scaled according to exposure
time and subtract 7 DN.
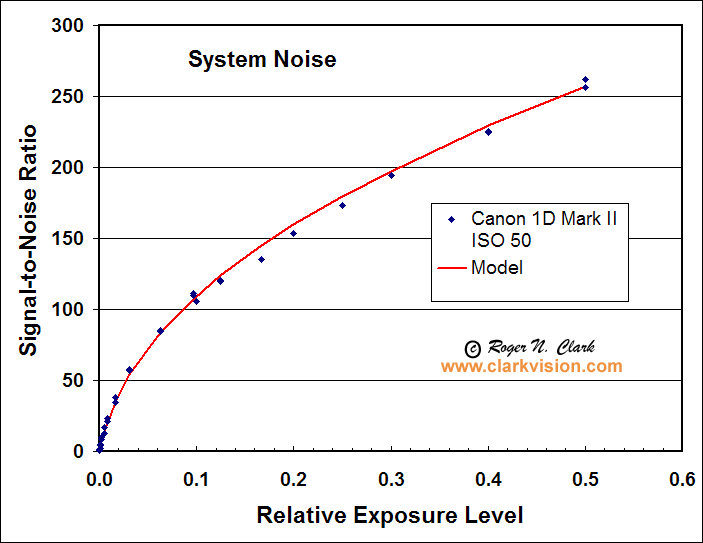
Figure 2. Signal-to-noise ratio observed and predicted. The prediction
model uses photon statistics and read noise.
Model is average DN scaled to electrons plus read noise. For this case,
ISO 50, the gain is 26.03 electrons/DN, and the read noise is 30.62 electrons.
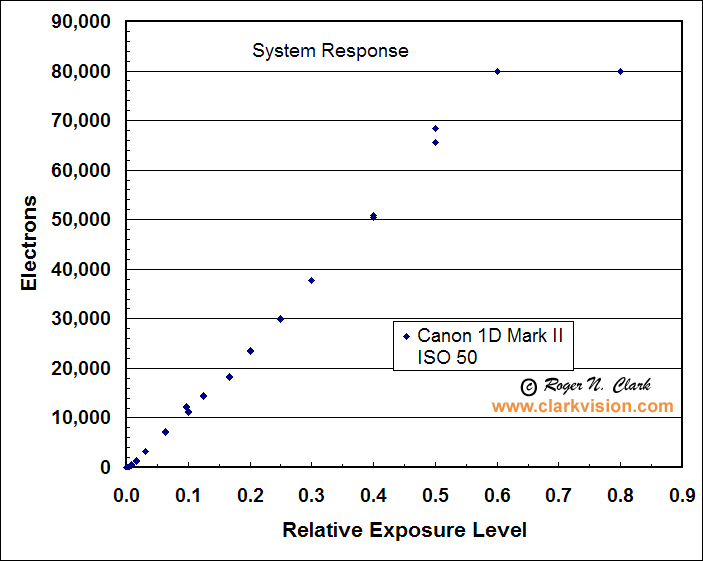
Figure 3. The electrons converted by the canon 1D Mark II sensor
are shown relative to exposure level. The sensor saturates at about
79,900 electrons, but is quite linear below that level.
Noise Sources
The "read noise" in Tables 1a and 1b vary with ISO and have been
a source of confusion to phtographers reading these results.
The analog-to-digital converter (A/D, or ADC) used in the Canon 1D Mark II
is 12-bits. Noise specifications for typical 12-bit A/Ds running
in the tens of megahertz range are expressed in decibels (dB)
and typically give about a 70 dB signal-to-noise ratio.
Twelve bits if perfect would give 72.2 dB (=20 log(4095)), so
70 dB is very good. In Figure 4, the noise floor is modeled as
a function of ISO, using the data in Table 1a. Only 2 noise sources
are needed to model the observed noise: a base level of sensor read noise
that is constant at all ISOs, and a constant 70.5 dB of
noise-to-noise ratio from the
A/D converter. This illustrates that newer cameras employing
14-bit converters should have improved performance at low
ISO. The Figure also illustrates one should use ISOs of 800 or higher
for low light work, because the noise is dominated only by sensor
read noise.

Figure 4. Camera noise sources for fast shutter speeds
are well modeled with only two sources: sensor read noise and
noise from the analog-to-digital converter.
The noise model is the square root of the sum of the squared
noise sources (A/D signal-to-noise ratio = 70.5 dB
and the sensor read noise =3.8 electrons).
The observed noise are the values from Table 1a, column F.
Dark Current and Related Noise
Another noise component is due to dark current, which will
increase with exposure time. Dark current and its noise is
also a function of the temperature of the sensor and associated
electronics.
Dark current was measured at room temperature for 623 and 1800 second
exposures at ISO 1600. Pairs of images were analyzed similar to that
done for read noise. There is not a clean answer because as exposure time
increases, dark current for each pixel is obviously quite variable,
resulting a large variation in signal. Long exposure images look
like they have a lot of noise spikes. Average dark currents were
measured at 0.013 to 0.02 electrons/second, but some pixels have
dark currents as high as about 0.25 electrons/second. In an 1800 second
exposure, that translates to signal levels of 23 to 450 electrons,
and noise of 5 to 21 electrons. It is this pixel to pixel
variation that limits the image quality of long exposures (Figure 4).

Figure 4. The noise in a 1D Mark II image is shown in this cropped
portion at full scale (1 camera pixel to 1 image pixel) for an
1800 second exposure at ISO 1600. Linear raw conversion in ImagesPlus 2.5.

Figure 5. A 623 second exposure of a target illuminated by only
0.00016 lux. The 1D Mark II camera was operating at room temperature
and ISO 1600 with a 50mm f/1.8 lens. This image has had no stretching
or processing other than raw image conversion in photoshop
with default settings, then the two rows cropped
from the full image and downsampled about 4x.
The width of the image is the full height of the original image.
The tilt of the target was intentional so image edges did not line up
with rows of pixels.
A test of a long exposure is shown in Figure 5. The 623 second exposure
at ISO 1600 shows some noise but is generally a very good image considering
the illumination was only 0.00016 lux (similar to an overcast night
away from cities with no moon; it took several minutes of dark adaption to
to begin to see the target in the room). The light detected is shown in
Table 3 along with the noise analysis and model prediction.
Table 3: Color Target Noise Statistics
Color
Chart
Patch |
Average
Intensity
(Photons) | Photon Rate
(Photons per
pixel/second)
| Measured
Noise
(electrons) | Noise
Model
(electrons) |
| A | 749.4 | 1.21 | 26.9 | 30.3 |
| B | 494.9 | 0.794 | 24.0 | 25.8 |
| C | 288.7 | 0.463 | 22.7 | 21.4 |
| D | 148.5 | 0.238 | 21.4 | 17.9 |
| E | 60.6 | 0.097 | 21.2 | 15.2 |
| F | 19.4 | 0.031 | 16.8 | 13.8 |
The data in Table 3 shows that DSLRs like the 1D Mark II can operate at
very low light levels at room temperature. The noise model is:
N = (P + r2 + t2)1/2, (eqn 2)
Where N = total noise in electrons, P = number of photons, r = read noise
in electrons, and t = thermal noise in electrons. Noise from a stream of
photons, the light we all see and image with our cameras, is the square root
of the number of photons, so that is why the P in equation 2 is not squared
(sqrt(P)2 = P). The model used the read noise of 3.9 electrons from
Table 1. The thermal noise squared = the dark current = 0.25 electrons/second * 623 seconds
= 157.75 electrons2.
Similar noise models are discussed in reference 6.
Pattern noise in long exposure dark frames is shown in Tables 4a, 4b and 4c.
| Table 4a. Thermal Noise, Central Image |
 |
ISO 1600
Exposure= 623 seconds
T= 20 C
Image Range:
-100.00 to 100.00 electrons about the mean
Central 500 x 300 pixel statistics:
min= 21 electrons
max= 3006 electrons
mean= 104 electrons
standard deviation= 48.77 electrons |
| Table 4b. Thermal Noise, Full Image, sub-sampled |
 |
ISO 1600
Exposure= 623 seconds
T= 20 C
Image Range:
-100.00 to 100.00 electrons about the mean
Full image statistics:
min= 6 electrons
max= 3006 electrons
mean= 106 electrons
standard deviation= 50.76 electrons |
| Table 4c. Thermal Noise, Full Image, sub-sampled |
 |
ISO 1600
Exposure= 623 seconds
T= 20 C
Image Range:
-20.00 to 20.00 electrons about the mean
Full image statistics:
min= 6 electrons
max= 3006 electrons
mean= 106 electrons
standard deviation= 50.76 electrons |
Conclusions
The data shown here for the Canon 1D Mark II shows that the camera is
operating and near perfect levels for the sensor. This means that for
high signals, noise is dominated by photon statistics. Noise at low
signal levels can be improved, but is very good. To achieve higher
signal-to-noise ratio images, a higher quantum efficiency sensor with
a larger full well would be needed. Without increasing the full well
capacity, the maximum signal-to-noise ratio would not improve, but that
the signal-to-noise ratio at ISO 50 could be achieved at higher
ISOs if the quantum efficiency were improved. Improvements in quantum
efficiency of 3 to 4x are possible (Reference 2).
The data for the 1D mark II indicate some important aspects for people
making images. The lowest ISO, 50, does have higher signal-to-noise ratios
than ISO 100, but at the expense of lower dynamic range and danger of
saturating highlights. An ISO of about 75 would be a better match
to the sensor range and would not sacrifice dynamic range. Unfortunately,
ISO 75 is not available.
For low light imaging, high ISO will record fainter light. There is no
advantage in using ISO 3200 and in fact there is a disadvantage in reduced
dynamic range. ISO 1600 is the optimum with the lowest read noise, but
ISO 800 is almost as good (almost the same read noise as ISO 1600) with
the advantage of almost double the dynamic range of ISO 1600.
Long exposures suffer from dark current that varies over a factor of
ten from pixel to pixel, ultimately limiting image quality of long
exposures. If dark current could be made more uniform, much longer
exposures could be made with high image quality. Even so, 10+ minute
exposures at ISO 1600 still produce acceptable images, recording
only a few photons.
With the details of how to evaluate sensor noise presented here, everyone
can evaluate their own cameras. For other descriptions, see References
1 and 3.
If you find the information on this site useful,
please support Clarkvision and make a donation (link below).
References
1)
CCD Gain. http://spiff.rit.edu/classes/phys559/lectures/gain/gain.html
2)
Charge coupled CMOS and hybrid detector arrays
http://huhepl.harvard.edu/~LSST/general/Janesick_paper_2003.pdf
3)
Canon EOS 20D vs Canon EOS 10D and
Canon 10D / Canon 20D / Nikon D70 / Audine comparison
http://www.astrosurf.org/buil/20d/20dvs10d.htm
4)
http://www.photomet.com/library_enc_fwcapacity.shtml
5)
Astrophotography Signal-to-Noise with a Canon 10D Camera
http://clarkvision.com/astro/canon-10d-signal-to-noise
6)
Concepts in Digital Imaging Technology
CCD Noise Sources and Signal-to-Noise Ratio
http://learn.hamamatsu.com/articles/ccdsnr.html
7)
dcraw. http://www.cybercom.net/%7Edcoffin/dcraw
8)
dcraw manual page.
9)
dcraw downloads.
Notes:
DN is "Data Number." That is the number in the file for each
pixel. I'm quoting the luminance level (although red, green
and blue are almost the same in the cases I cited).
16-bit signed integer: -32768 to +32767
16-bit unsigned integer: 0 to 65535
Photoshop uses signed integers, but the 16-bit tiff is
unsigned integer (correctly read by ImagesPlus).
http://clarkvision.com/reviews/evaluation-1d2
First published July 8, 2007.
Last updated January 18, 2014








