
The Canon S70 Digital Camera Review:
Sensor Noise, Dynamic Range, and Full Well Analysis
by Roger N. Clark
All images, text and data on this site are copyrighted.
They may not be used except by written permission from Roger N. Clark.
All rights reserved.
This page shows an analysis of noise, dynamic range, and full well capacity
of a Canon S70 camera.
Procedures for performing this analysis are described in:
Procedures for Evaluating Digital Camera Noise, Dynamic Range, and Full
Well Capacities; Canon 1D Mark II Analysis
The lowest possible noise from a
system detecting light is the noise due to Poisson statistics
from the random rate of arrival of photons. This is called
photon statistics, or photon noise. Noise from the electronics
will add to the photon noise. We will see that
the noise in Canon S70 images is limited by photon statistics at high
signal levels and by electronic noise from reading the sensor
(called readout noise) at very low signal levels.
In the case of high signal levels, a system that is photon statistics
limited enables us to directly measure how many photons
the sensor captures, and by increasing the exposure, we can
determine how many photons are required to saturate the
sensor. That is called the full well capacity.
With data on the lowest noise to the highest signal, we can then
determine the dynamic range of the sensor.
Results
Results for determining read noise, gain, dynamic range and maximum
signal-to-noise ratio are shown in Table 1. Column B is the
gain derived from high signal data. Gains at ISOs
higher than 50 are scaled relative to that at ISO 50. Read noise,
Column C was determined from exposures with zero light on the sensor.
Maximum signal, column D, is 8,200 electrons at ISO 50 for the Canon S70.
That maximum occurs at a signal level just below maximum A-to-D converter
output 3965/4096 in 12-bit data numbers (DN).
Dynamic range, Column E = maximum signal / read noise, and column
F shows that range in photographic stops.
Higher ISO reduces the maximum electrons (photons) that are recorded
relative to ISO 50 (e.g. ISO 400 sees half the electrons of ISO 200).
The maximum signal-to-noise ratio, Column g, is the square root of the
number of maximum photons recorded (e.g. square root 670 at ISO 200 = 46)
(read noise is negligible for the high signal case).
Table 1: Canon S70: Derived Sensor Performance
A B C D E F G
Camera Apparent
ISO Gain Read Noise Maximum Dynamic Dynamic Maximum
(electrons/ (electrons) Signal Range Range Signal-to-Noise
12-bit DN) (electrons) (linear) (stops) Ratio
50 2.06 4.1 8,200 2000 11.0 91
100 1.03 3.4 4,300 1260 10.3 66
200 0.51 3.2 2,150 670 9.4 46
400 0.26 4.3 1,080 250 8.0 33
An important factor in high ISO performance is collecting enough
photons. Small pixels have difficulty doing just that.
The direct effect of the number of photons collected is the gain
needed to convert the signal from a pixel to a digital number.
The gain of the camera is given in column B in Table 1. Once
gain drops below 1 electron/DN, there is little point in
increasing ISO further. On the Canon S70, unity gain
occurs at about ISO 100. Thus, the effect of higher
ISO only decreases dynamic range without helping to detect lower
signals. For comparison, unity gain of some large pixel DSLR
cameras (e.g. the Canon 1D Mark II) occurs around ISO 1300,
indicating the DSLR collects
13 times more photons than the S70 for the same f/ratio lens
and exposure time. In other words, the DSLR is about 13 times more
sensitive. Another interesting property to compare with the
DSLR is pixel area: the S70 has 2.3 micron pixel pitch, while the
Canon 1D Mark II has an 8.2 micron pitch, and the ratio
of the areas is (8.2*8.2)/(2.3*2.3) = 13, thus matching the
difference in sensitivity.
The system linearity is shown in Figure 1, and
is very good. System linearity includes the detector
linearity, shutter reproducibility, f/stop reproducibility, and light
source stability.
The signal-to-noise ratio as a function of intensity is
shown in Figure 2. If the sensor is photon noise limited, the trend
in this ratio is a square root dependence.
If the system is photon noise limited, the signal-to-noise
ratio squared directly equals the number of photons collected
without needing gain conversions, or computing the slope of a line.
The fact that the model matches the data very well indicates
there are no other sources of noise contributing to the data at any
significant level. Thus, for high signal levels, the Canon S70 is
photon noise limited. This means further improvements in electronics
will not improve the signal-to-noise ratio for high signal levels.
If the quantum efficiency were improved with a different sensor, that
would certainly improve the signal-to-noise ratio.
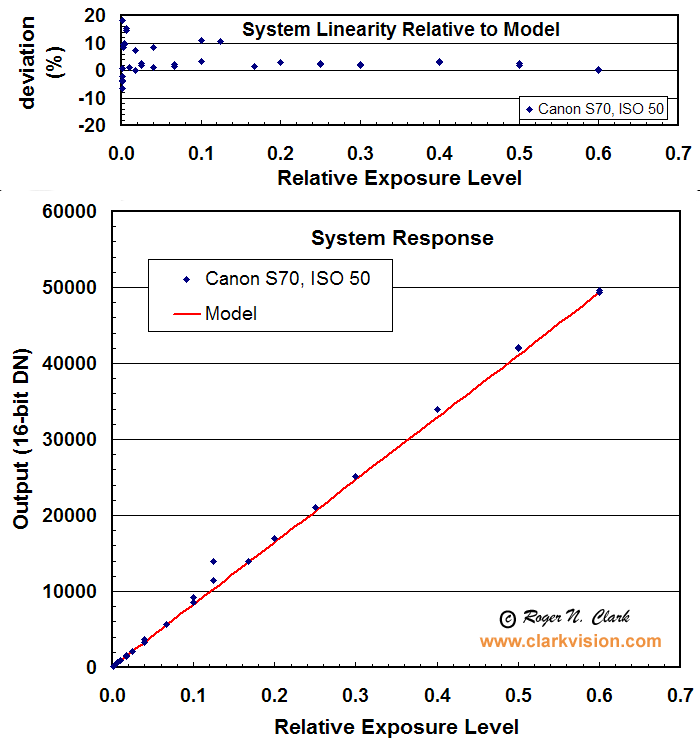
Figure 1. The Canon S70 shows a very linear trend with signal.
Variations in signal level include repeatability of the shutter and aperture,
as well as the light source.
The model is the average high signal DN scaled according to exposure
time and subtract read noise.
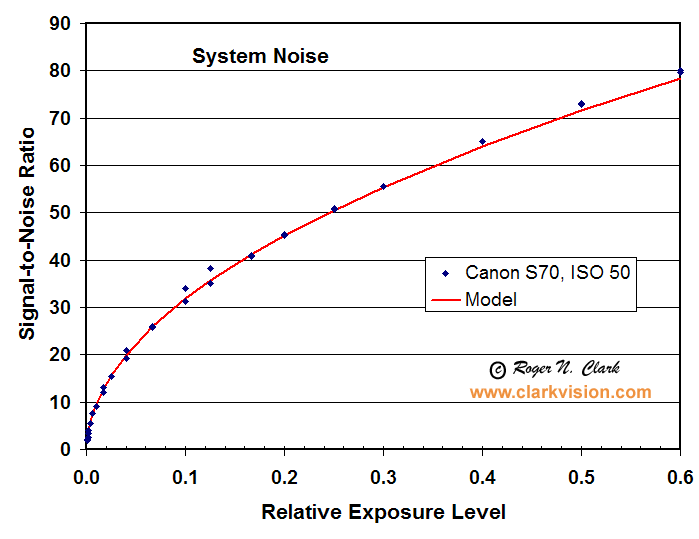
Figure 2. Signal-to-noise ratio observed and predicted. The prediction
model uses photon statistics and read noise.
Model is average DN scaled to electrons plus read noise. For this case,
ISO 50, the gain is 2.06 electrons/camera DN (4096 levels), and the read
noise is 4.1 electrons.
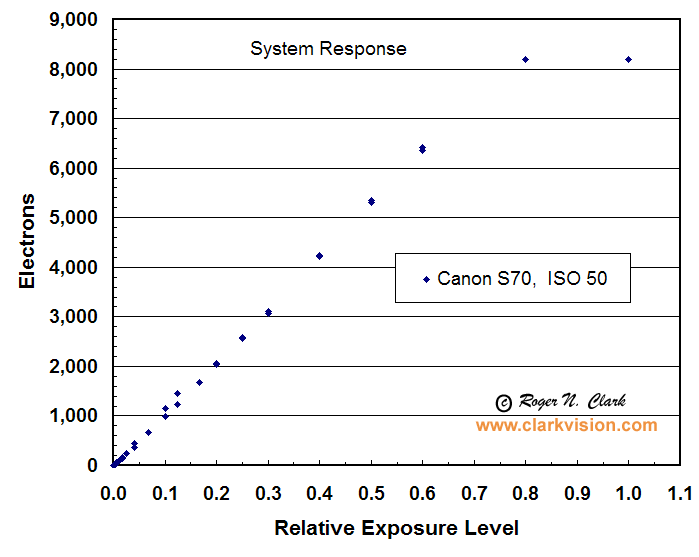
Figure 3. The electrons converted by the Canon S70 sensor
are shown relative to an arbitrary exposure level. The
sensor saturates at about
8,200 electrons, but is quite linear below that level.
Dark Current and Related Noise
Another noise component is due to dark current, which will
increase with exposure time. Dark current and its noise is
also a function of the temperature of the sensor and associated
electronics.
Data to be added.
The noise model is:
N = (P + r2 + t2)1/2, (eqn 1)
Where N = total noise in electrons, P = number of photons, r = read noise
in electrons, and t = thermal noise in electrons. Noise from a stream of
photons, the light we all see and image with our cameras, is the square root
of the number of photons, so that is why the P in equation 1 is not squared
(sqrt(P)2 = P).
Conclusions
The data shown here for the Canon S70 shows that the camera is
operating and near perfect levels for the sensor. This means that for
high signals, noise is dominated by photon statistics. Noise at low
signal levels is quite good and would be very difficult to improve
further. In fact, the read noise is extremely low, even lower than that
measured on some DSLR cameras at similar ISOs. The low read noise,
below 4 electrons at ISO 100 and 200, is very impressive! To achieve higher
signal-to-noise ratio images, a higher quantum efficiency sensor with
a larger full well would be needed. Without increasing the full well
capacity, the maximum signal-to-noise ratio would not improve.
Improvements in quantum
efficiency of about 3 are possible (Reference 2), but currently that
would require much more expensive detectors, such as back-side
illuminated CCDs. Note DSLRs have maximum full well capacities
on the order of 50,000 electrons (e.g. Canon 20D) to 80,000
electrons (e.g. Canon 1D Mark II). Thus a factor of 3 improvement
in quantum efficiency and full well capacity (3*8200 = 24,600 electrons)
for the Canon S70 would still not match that found in large pixel DSLRs.
For comparison with a large pixel DSLR, compare Table 1 and the figures
with that for the
Canon 1D Mark II Analysis.
References
1)
CCD Gain. http://spiff.rit.edu/classes/phys559/lectures/gain/gain.html
2)
Charge coupled CMOS and hybrid detector arrays
http://huhepl.harvard.edu/~LSST/general/Janesick_paper_2003.pdf
3)
Canon EOS 20D vs Canon EOS 10D and
Canon 10D / Canon 20D / Nikon D70 / Audine comparison
http://www.astrosurf.org/buil/20d/20dvs10d.htm
4)
http://www.photomet.com/library_enc_fwcapacity.shtml
5)
Astrophotography Signal-to-Noise with a Canon 10D Camera
http://www.clarkvision.com/astro/canon-10d-signal-to-noise
Notes:
DN is "Data Number." That is the number in the file for each
pixel. I'm quoting the luminance level (although red, green
and blue are almost the same in the cases I cited).
16-bit signed integer: -32768 to +32767
16-bit unsigned integer: 0 to 65535
Photoshop uses signed integers, but the 16-bit tiff is
unsigned integer (correctly read by ImagesPlus).
Back to:
Digital Camera Sensor Analysis pages on this site:
http://www.clarkvision.com/articles/index.html#sensor_analysis
http://www.clarkvision.com/reviews/evaluation-canon-s70
First published September 15, 2006.
Last updated September 16, 2006


