Is there an optimum signal-to-noise ratio with the Canon 10D camera for astrophotography (or any low-light photography)? Is higher ISO better (more signal), or is there too much noise? Are longer exposures better (more signal) or does noise begin to increase faster than the signal? Here are some results from experiments.
The test involved placing the camera in a dark room or outside at night and taking a series of exposures with various ISO and exposure time settings, from 1/2000 to 359 seconds. The lens cap was left on, so the series recorded dark frames. There was approximately 15 seconds between exposures at 70 F and 30 seconds at lower temperatures. All data were recorded in raw mode and converted using the raw converter in ImagesPlus 1.71, linear mode. Statistics were obtained with ImagesPlus 1.71
The basic data from the 70 degree F tests are shown in Figure 1.
Tests at 70 degrees F
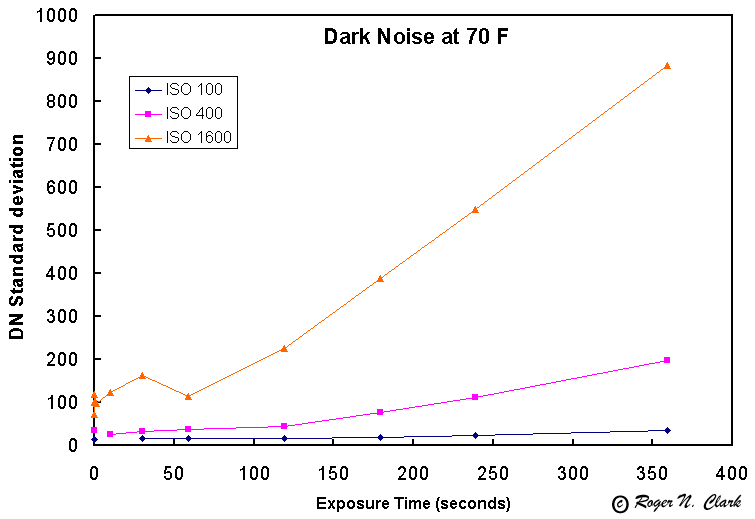
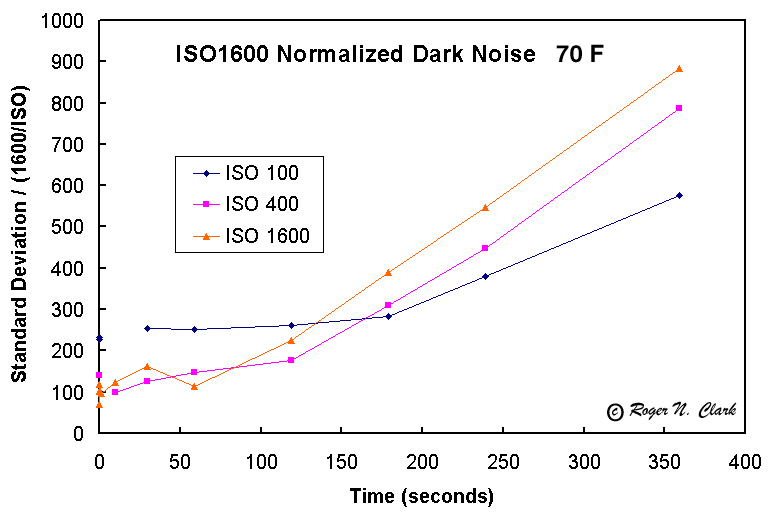
If we scale the noise by the ISO settings, we can see the relative noise in Figure 2. This plot shows that for longer exposures, you will achieve a better signal to noise by using lower ISO settings. Of course this is at 70 F. At lower temperatures, the situation changes.
What we really want to know, is for a given total exposure time, what ISO and what individual exposure times are best, assuming multiple exposures are co-added. Figure 3 answers this question for a temperature of 70 F.

Figure 3 shows that at 70 F you can achieve the highest signal-to-noise by taking ISO 1600 1-minute exposures. Thus, if you want 10 minutes total exposure, take ten 1-minute ISO 1600 exposures. If you go longer than 1-minute in each exposure, then lower ISO settings are best. For example, at ISO 400, five 2-minute exposures would be best and produce about 90% the signal-to-noise of ten 1-minute exposures at ISO 1600. Mote, however, that higher ISO settings have greater peak noise. Thus, considering peak noise and standard deviation in Figure 3, I would choose the ISO 400 2-minute exposures. While the average noise would be about 10% less, the peak noise would be about 1.4 (square root 2) lower. More about peak noise below. When the noise in Figure 3 between 2 curves is less than about 40% difference, the lower ISO setting will probably give a better result considering peak noise. This means at both 1 and 2-minute exposures, the ISO 400 will give better overall results at 70 F.
Tests at 51 degrees F
As the temperature of the camera and its sensor drops, the noise decreases, but the gain stays constant (exactly how constant needs to be tested). Thus, the signal to noise increases as temperature drops. Below shows the results as described above, except at 51 degrees F. For the tests at this temperature, the wait time between dark frames was increased to 30 seconds.
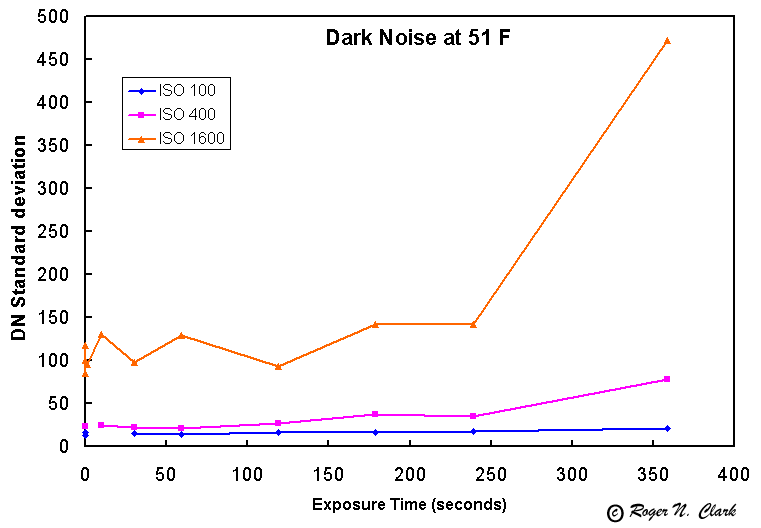
Compare Figure 4 with Figure 1. The noise has dropped significantly for both 400 and 1600 ISO settings, but has not changed much at ISO 100. This is reflected in the normalized ISO dark plots in Figure 5.
In Figure 5 we see that the normalized noise at both ISO 400 and 1600 are similar, meaning there should be no signal to noise advantage between these settings for a given total exposure time, up to about 4-minutes exposure time. After about 4 minutes, the noise at 1600 starts to increase more rapidly.
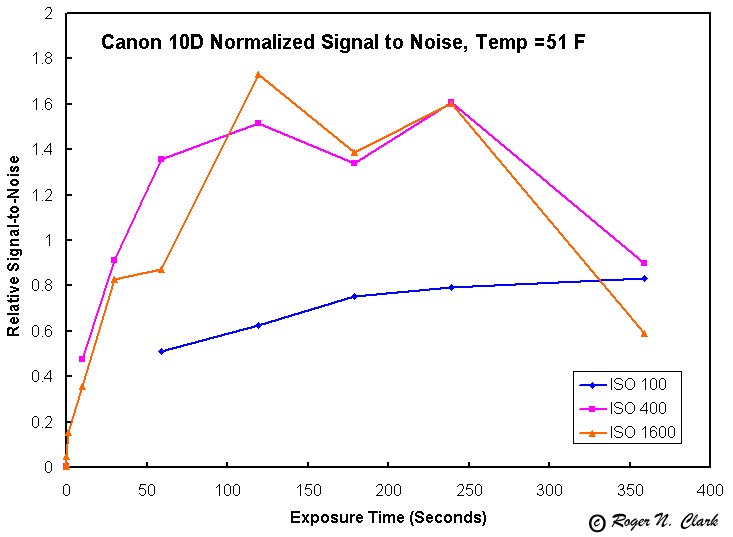
The relative signal-to-noise shown in Figure 6 is scaled relative to the signal-to-noise achieved at ISO 1600, 59-second exposure, 70 F from Figure 3. Thus, the data in Figure 6 are directly comparable to that in Figure 3. We see that the signal-to-noise ratio is substantially improved at 51 F compared to 70 F, as expected. But the maximum in signal-to-noise broadens and shifts to longer exposure times. Also, both ISO 400 and 1600 give essentially equivalent signal-to-noise ratios from about 2 to 4 minutes, but the signal-to-noise drops rapidly after 4 minutes. For exposures greater than 6 minutes, ISO 100 will probably give a greater signal to noise than the high ISO settings.
What is not shown in the Figure 1-6 plots is peak noise. The peak noise is about 6 to 12 times higher than the standard deviation, and will cause "speckles" in final images. For example, at 239 seconds exposure at 51f, the peak as ISO 1600 was found to be 1541 (excluding hot pixels), while at ISO 400 was only 401, almost 4 times less. At 119 seconds exposure, the peak numbers drop to 739 as ISO 1600 and 268 at ISO 400 almost three times less. But which is better?
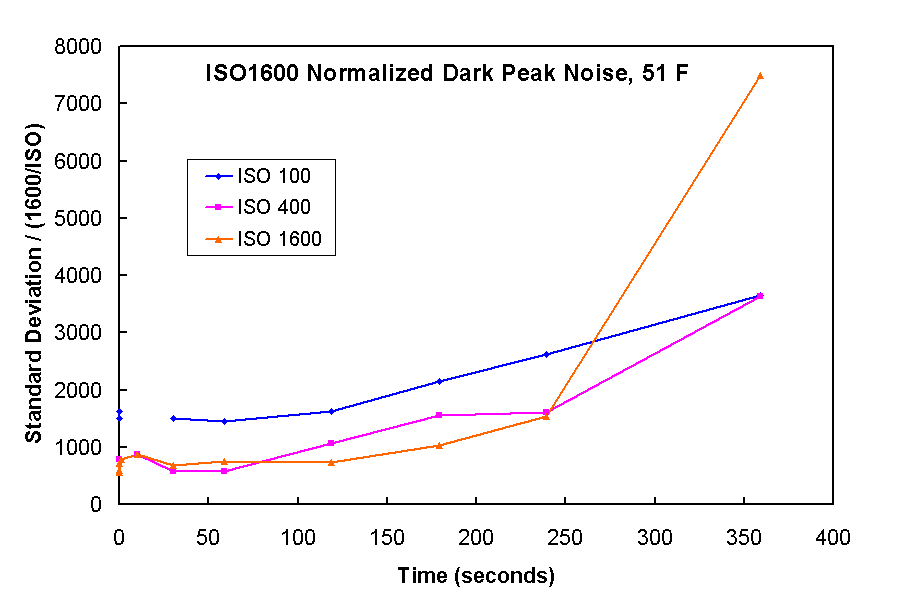
Peak Noise at 51 F is shown in Figure 7. While it is 6 to 12 times higher than the standard deviation of the noise, we must consider gain (ISO) on the signal ad the signal to noise achievable from peak noise as compared to the standard deviation of the noise. After all, spurious peaks will add "speckles" to the image and could be confused with faint stars.
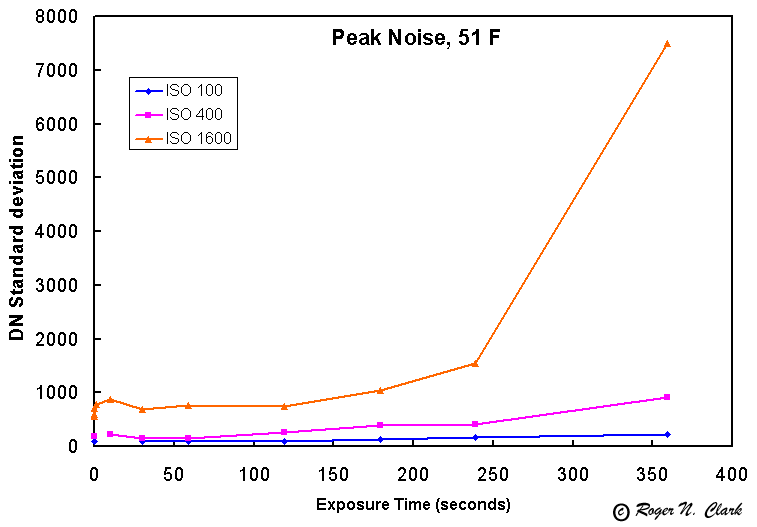
Normalizing the peak noise in Figure 8, we see that while high ISO gives higher peak noise than low ISO settings, high ISO also gives high signal. Thus relative to peak noise, higher ISO seems to be winning.
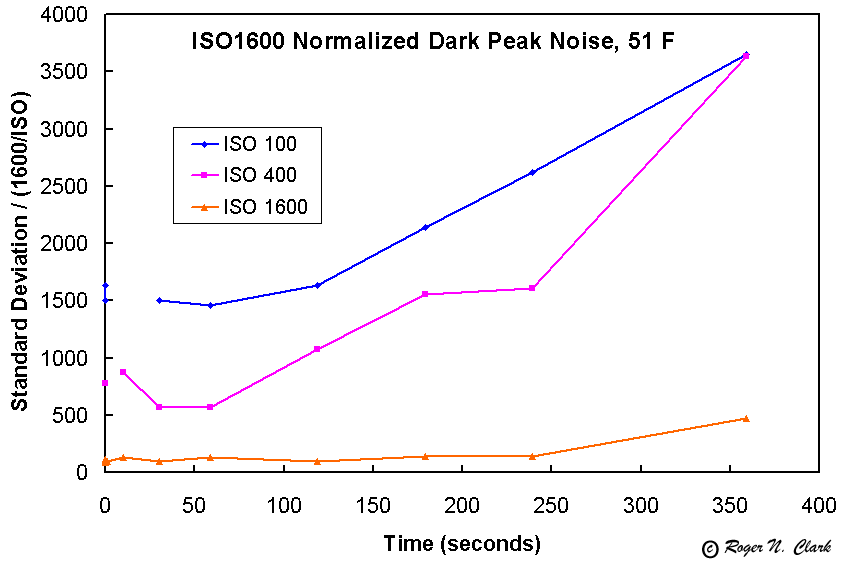
Computing the achieved signal-to-noise ratio on a relative scales from Figure 3, (again relative to the signal-to-noise ratio achieved at 70 F, ISO 1600 standard deviation), we see a different picture. Now we see ISO 1600 producing the best result for about 2-minute exposures at 51 F. Considering Figures 6 and 9, we see that ISO 1600 to gives the best signal-to-noise ratio for both standard deviation and peak noise.

The data in Figure 6 show a need to test ISO 200.
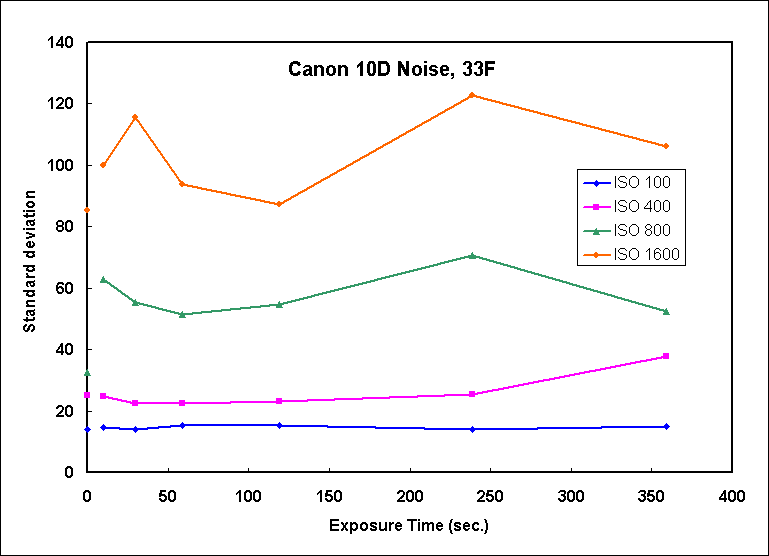
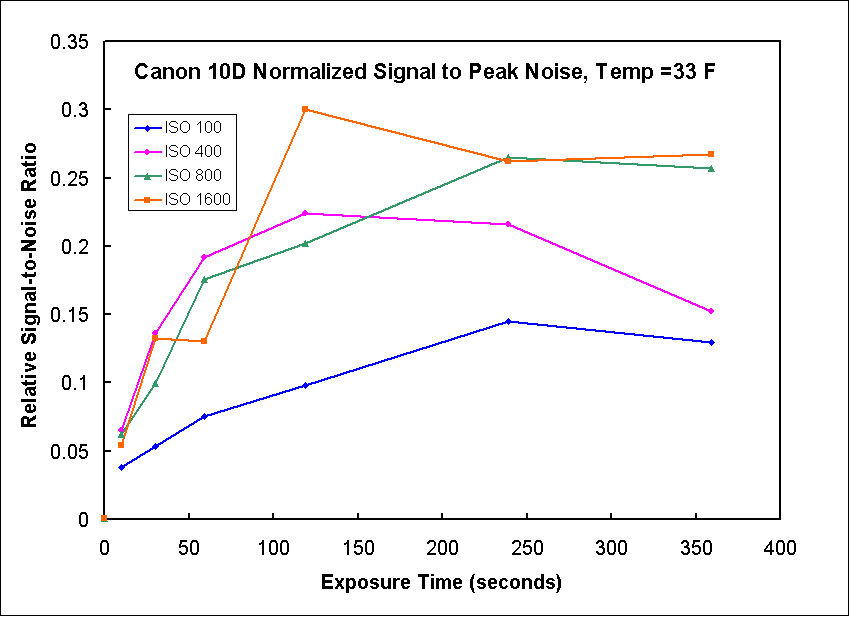
Next we look at tests done at a temperature of 33 F. The noise at 33F, Figure 10, is relatively constant for different exposure times. In Figure 11 we see that when we normalize the ISO, only ISO 100 has high relative noise. ISO 400 to 1600 produce similar noise which scales proportionally with gain (ISO). Figure 13 shows the relative signal to noise ratio. It shows that ISO 400, 800 amd 1600 will produce about the same results at any total exposure and that exposures from 2 to 6 minutes work well.
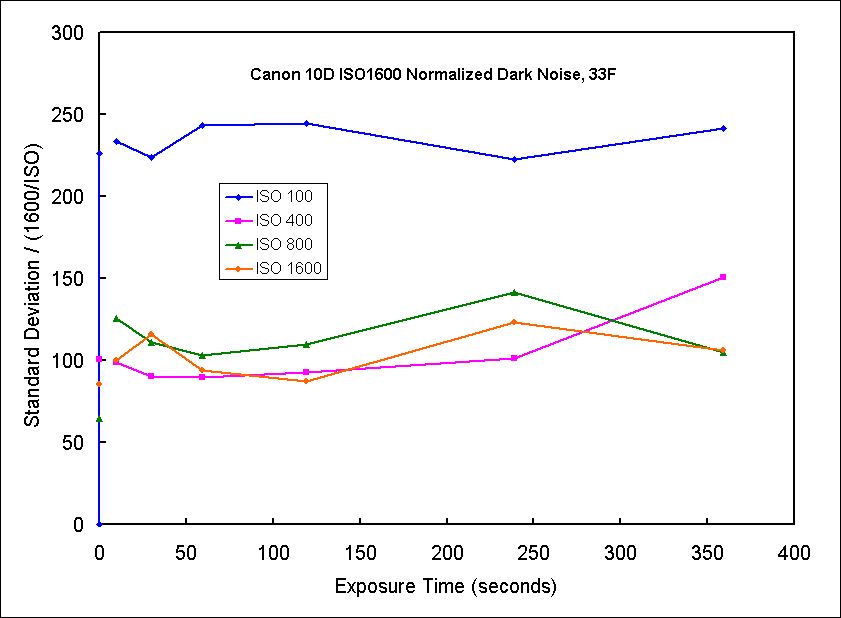
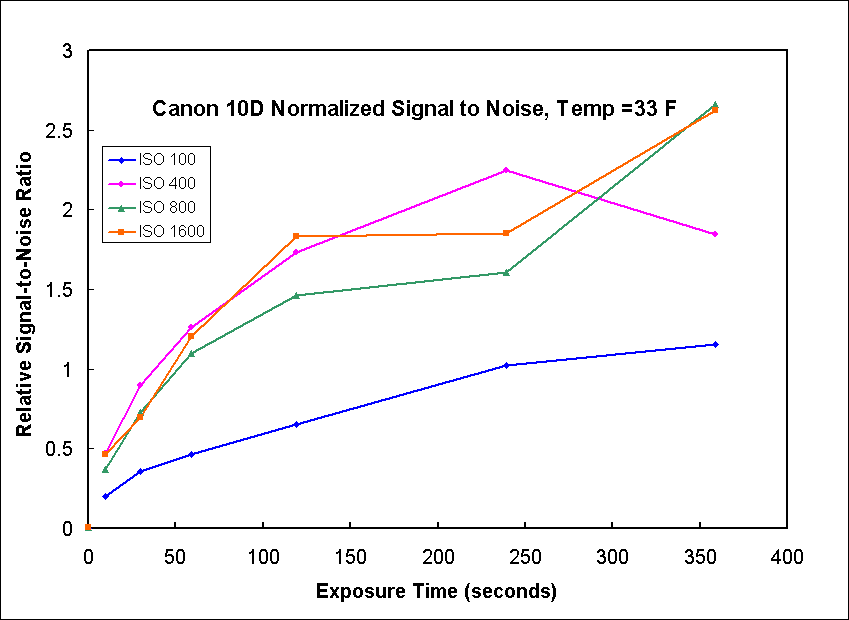
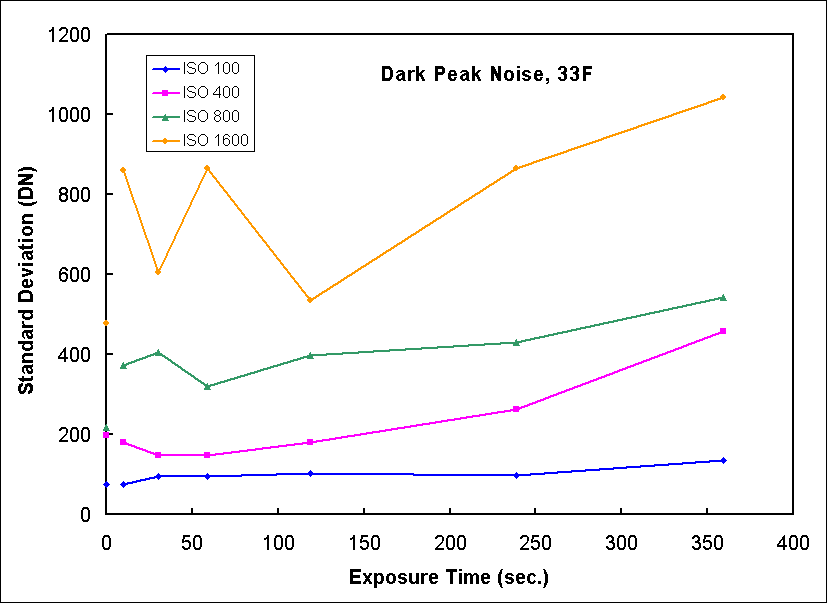
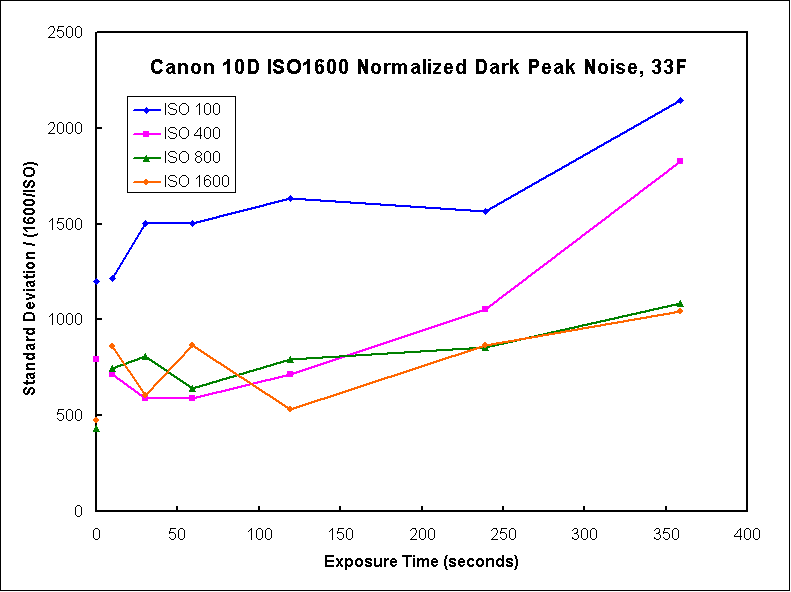
Now lets look at data for peak noise at 33 F. Figure 13 shows the peak noise is relatively constant with exposure time up to 4 minutes then begins to increase. The normalized peak noise, Figure 14, shows higher ISO values produce similar relative noise levels. Only at 6 minutes does the ISO 400 show higher relative noise, approaching that for ISO 100. The relative signal to noise ratio, Figure 15, shows a relative maximum in the 2 to 4 minutes range, but still increasing or doing well at 6 minutes.
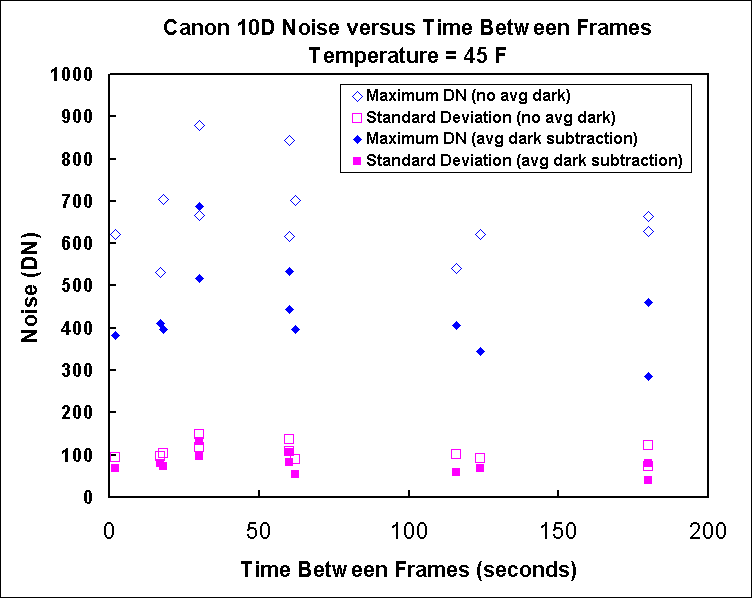
Some of the data above seems to jump around. One possibility is variable times between exposures. When in operation, the camera generates heat and by letting the camera rest between exposures it might cool. Figure 15 shows the noise as a function of time between frames. The camera turned off after 2 minutes, so at 3 minutes, the camera is off for the last minute. We see there is little change in levels from short to long times between exposures. Shorter rest times seem to have more range in the statistics, but there is no clear downward trend. Thus, instead of waiting between exposures, this data says to continue framing as that builds signal. A minimum wait time depends on the write speed of a card, but 12 to 15 seconds should be enough to write raw data unless the memory card is very slow. The variability in the numbers shows that the data are inherently variable. Consider this variability when examining what is significant in all the plots on this page.
In computing signal to noise (S/N), I assume signal increases linearly with exposure time and ISO (it does in the experiments I've done). Thus, I compute a virtual signal based on ISO and exposure and compare that to the measured noise. I scaled the number for 70F peak to come out about 1.0 and then use the same scale factors for all other tests. So all other S/N plots are relative to that level. So Figure 12 shows levels around 2 meaning that the 33 F provides a S/N about twice that at 70 F. But the peak noise at 33 F (Figure 15) is only about 0.3 that for standard deviation noise at 70 F.
Conclusions
From the data collected so far, it appears that at temperatures near 70 F, the highest signal-to-noise ratio data, considering both standard deviation and peak noise, would be obtained with 1-minute exposures at ISO 1600, stacking multiple exposures to achieve the desired total integration time. Two-minute exposures at ISO 400 will provide nearly the same results. At 51 F, again ISO 1600 would provide the best results with exposures of about 2 minutes, stacking multiple exposures to achieve the desired total integration time. Again, ISO 400 with 2 to 4-minute exposures will produce similar results. Since ISO 800 has not yet been fully tested, it might be a good compromise between noise and longer exposures, as indicated by the experience of many astro-imagers. At 33 F, 2 to 6 minutes all produce excellent results.
Delays between exposures are not necessary to let the camera cool, at least at 45 F with a slight breeze. This test series implies use a low delay time, but enough to let the camera write data to the memory card.
Other considerations: the signal to noise tests are for the limit of detection. If you have a strong signal, you will get a better looking image using lower ISO settings, but the image may not reach as faint. For example, for bright subjects like the Orion Nebula, M42, lower ISO settings may still give a strong signal and the image will appear with less noise. The results concerning maximum signal to noise are for bringing out the faintest details.
Notes
The tests were done using ImagesPlus Canon raw file converter, then using ImagesPlus cursor read routine with a box of 29x29 pixels at location (999,999) to get statistics. That location seemed representative of the data without any hot pixels for my camera. All data were obtained in raw mode and converted with ImagesPlus 1.71 to 16-bit tif files. Numbers refer to 16-bit tif DNs from ImagesPlus.
NOTE: Figures 7,8 and 9: the vertical axis says standard deviation, but it should read Peak Noise. I'll change it when I have time.
Equations Used
The reason you do not need to measure a signal is because we know the sensor is linear and absolutely calibrated. We know that it is absolutely calibrated because it is calibrated to the ISO standard. We know that the signal is proportional to iso times exposure time. Simply measuring the noise is the lowest we can possibly get. If we use a signal just above the noise to calculate signal to noise, then we will be adding in photon statistics. So, knowing signal is proportional to ISO and exposure time, we can calculate a virtual signal of any level we want.
The reason to normalize the noise is a way to compare the noise without gain factors. Look at Figure 1 above and you see the noise all plot different lines. If ISO were simply a digital gain, the curves would plot on top of each other. But if the noise were system limited, the curves would also plot on top of each other. In Figure 2, we see the ISO 100 curve is constant, then rises for exposures greater than 180 seconds exposure. This says the system is read noise limited below 180 seconds at iso 100. The iso 400 and 1600 curves plot about the same, and have a flat region below about 60 seconds. That says at iso 400 and higher, noise is well digitized, and is read noise limited below 60 seconds.
But in Figure 2, signal increases with exposure time, so to calculate signal-to-noise, one must divide a virtual signal by the noise. The signal increases linearly with exposure time, so signal to noise is proportional to iso * exposure time / noise for that exposure time. But that is also not what we want. We want to know for a given exposure time, is it better to do one long time, two, three, or many shorter exposures that add up to the total. So I normalized the total exposure time to 10 minutes (600 seconds). If you measure the noise from a single 5-minute exposure, and you want to scale to a 10-minute exposure, then the signal-to-noise would increase by square root 2 because you need two measurements. So the relative signal-to-noise should be scaled by the square root of the number of exposures needed to reach the reference exposure time (this is the square root (C/T) below.
The equations are:
NN = N*(1600/ISO)
RSN = K/(N*(1600/ISO)*sqrt(C/T))
where
ISO = the "film" speed,
N = standard deviation of the noise
NN = normalized noise,
RSN = relative signal-to-noise,
K = Scaling Constant (set to 360 in my tests)
This just scales the answer to some level,
I chose the reference level to be the 10D
at ISO 1600, 60 second exposure so RSN=1.0.
If K=360, all other camera calculations
would be relative to this (including different
model cameras). This also assumes 16-bit
scaled data from the camera in linear mode.
(note photoshop is 15-bit)
C = reference exposure time scaling constant, chosen
to be 600 seconds.
If C is changed from 600, then K must be changed
to keep an overall reference to inter compare
different systems.
sqrt= square root function.
Last updated January 29, 2005.