| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
by Roger N. Clark
This is part 2 of illustrating image sharpening methods.
The series:
Introduction to Sharpening
Unsharp Mask
Part 1
Part 2
Part 3.
Introduction
Image sharpening is usually desired in post processing digital images, but not all sharpening methods are equal. In this example, we will start with a high signal-to-noise ratio image, then intentionally blur it, and try to restore and/or surpass the detail in the original unblurred image. Because we are adding the blur, we have the unblurred image so we can check if a given methodology produces artifacts or not. In this example, I will show about a 2x improvement in resolution in the image, producing a much sharper image than the blurry starting image.
Comparison of Unsharp Mask, Smart Sharpen, and Richardson-Lucy image deconvolution
The three methods tested used Photoshop CS5 for the Unsharp Mask and Smart Sharpen tools and ImagesPlus for the Richardson-Lucy image deconvolution. Figures 1, 2 and 3 show the blurred image on the left and the sharpened image on the right. The test image is that of a crowned crane obtained in Tanzania using a Canon 1D Mark IV digital camera and 300 mm f/2.8 lens. The original image was downsized using 3x3 pixel binning which improves signal-to-noise ratio by 3x and produces a very sharp image. The original image is shown on the left in Figure 4.
Blurring used Photoshop's Gaussian blur with radius = 2. This combination produces a blur close to that from a slightly out of focus image combined with the blur filter on the camera and lens aberrations. The blur on a single pixel point source is shown as an inset in Figures 1, 2, and 3. This profile is similar to some star images I see when I do night photography and focus is slightly off or there is some atmospheric turbulence. The blur is also similar to what I see in slightly out-of-focus parts of a wildlife or landscape image (e.g. just slightly outside the depth of field). The Gaussian blur results in a Full Width at Half Maximum of a blurred point source = 4 pixels. This results in a near zero Modulation Transfer Function (MTF) in pixel to pixel line detail). What this means is there would be no discerning closely spaced lines in the image and virtually no pixel to pixel detail (not to be confused with an intensity gradient).
The blurred image (e.g., Figure 1, left) is the type of image I would consider not quite sharp enough, and if I only used unsharp mask or smart sharpen, it would not be a sharp enough image for me to keep and display in most cases. Let's now look at results from attempting to sharpen the blurred image.
If you can not readily see the differences between the left and right images in Figures 1, 2, and 3, enlarge the images (e.g. 200%) or use a different monitor. If the images on the right do not look significantly sharper in Figure 3, perhaps you need a new monitor, as the differences should appear striking.
What is Sharpness?
The perception of sharpness in an image contains several factors. One is how much from pixel to pixel the intensity changes. For example in the blurred image on the left in Figure 1, the transition from the white feathers on the bird's cheek to the black feathers occurs over several pixels. That means we perceive the image as soft. But a hard edge (e.g. white to black in one pixel) is only part of sharpness. Now look at the catchlight in the bird's eye. The catchlight also appears soft. Same with bright spots on the bird's bill, and structure in the birds feathers. These image components are spread out. It is not just the transition over several pixels, but the size of the strictures. A sharp image includes small components, the fine detail, down to the limit of vision. Thus, it is the size of the finest details that also contributes to our perception of sharpness. An image that contains both high accutance, and small details is considered sharp. A high accutance image that does not contain fine details might be considered sharp by some viewers but the image will pale in comparison to the same scene that also contains the fine details. In that comparison, the high accutance image would no longer be considered sharp compared to the image with both high accutance and fine details. Ideally, we could take an unsharp/blurry image and improve the fine details, actually improving image resolution and accutance. It can be done.
Contrary to some online posts that say it is not possible to
improve the resolution of images in post processing, there is a class
of algorithms that do just that. It is called image deconvolution.
I have included several scientific references at the end of the article.
There are over 4 decades of scientific research in this area and
image deconvolution is now used in many fields, from microscopy
to astronomy. The two classic papers in image deconvolution are:
Richardson (1972) and Lucy (1974) (see references), leading to the now
commonly used Richardson-Lucy deconvolution algorithm. That method is used here.
Deconvolution methods can, in some cases, improve resolution beyond
diffraction limits.
Sharpening Methods Compared
Unsharp Mask
The results from running unsharp mask on the blurred image is shown in Figure 1. The image on the right of Figure 1 shows the results of "sharpening" with unsharp mask. Of course one can push the unsharp mask further and do multiple runs, but the result is increasing artifacts. There is a small improvement in perceived image sharpness with unsharp mask, perhaps enough to keep the image, especially if it was a unique image. The unsharp mask has improved accutance (edge contrast), but has not improved fine detail (resolution). In fact, we shall see below that the size of some detail has actually grown larger, thus reducing resolution. Because of this fact, I say the unsharp mask does not actually sharpen.
Figure 1. Blurred image (left) compared to the processing of the blurred image
with unsharp mask (right). The amount of blur is illustrated by the small
black inset on the upper right of the left image. If there was no blur, the
inset would show only a single white pixel. The unsharp mask added
edge contrast, called accutance, to the image, making it appear sharper
but without increasing resolution.
Smart Sharpen
The smart sharpen tool in photoshop does more than just unsharp mask. In some modes it appears to do a one iteration deconvolution (I will try and find the reference that describes this). With only a single deconvolution step, the method is fast, but with limited results. The smart sharpen result produces a slightly better image than does unsharp mask on this image.
Figure 2. Blurred image (left) compared to the processing of the blurred image
with smart sharpen in Photoshop CS5 (right). The amount of blur is illustrated by the small
black inset on the upper right of the left image. The smart sharpen added
edge contrast, called accutance, to the image, making it appear sharper
but without any effective increase in resolution.
Richardson-Lucy Image Deconvolution
Figure 3. Blurred image (left) compared to the processing of the blurred image
with Richardson-Lucy image deconvolution (right). The amount of blur is illustrated by the small
black inset on the upper right of the left image. The result shows a wealth
of fine detail. Small objects have become smaller showing the improved resolution.
The blurred image was restored with Richardson-Lucy image deconvolution (Figure 3) using ImagesPlus. A total of 950 iterations were used. I purposely chose a Gaussian blur function different than what I used to blur the image, so that the inaccuracy might limit the result or produce artifacts. This simulates real-world conditions where one may not be able to determine the exact blur (called the point spread function), but it is usually possible to make an estimate of the blur. The result is much sharper than smart sharpen or unsharp mask. It is sharper in two important ways. Restoration of fine detail not perceptible in the blurred image, or in the unsharp mask and smart sharpen images, including detail smaller than the 0% MTF frequency of the Gaussian blurred image. Strictly speaking, one can't recover multiple parallel lines separated by less than the MTF=0 cutoff, but one CAN recover information on subjects smaller than the MTF=0 frequency with small details, like two close spots. Because real-world images are not parallel bar charts, one can, in practice, recover a lot of fine detail, even detail below diffraction limits using image deconvolution.
Figure 4 shows the original image, before blur, and the restored image (restored from the blurred image). One can compare the two to see that the recovered detail closely matches the original image. This proves that the recovered detail is real and not artifacts of the processing. In fact, I pushed a little further and the restored image has slightly more detail than the original. This process could go even further: the original image could be up sampled and then deconvolved to reveal even more detail. To do that, one needs a very high signal-to-noise ratio image.
Figure 4. Original image before blur (left) compared to the image restored
using Richardson-Lucy image deconvolution (right). The deconvolved
image (right) is the same image as that in Figure 3 (right). The deconvolved
image shows slightly more detail than the original and represents about
a 2x (linear) improvement in spatial resolution from the blurred image.
Figure 5. Example detail in the original blurred image (bottom) and
the restored image (top). A 49-pixel traverse is indicated by the
red line and results are shown in Figure 6. This image is enlarged 3x
using nearest neighbor. The top image is from the right image in Figures
3 and 4.
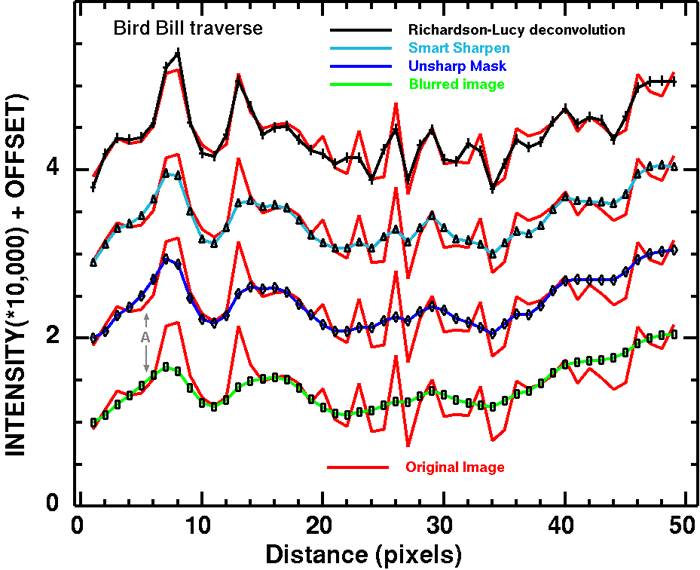
Figure 6. Traverse data along the line shown in Figure 5.
The red line in this plot is the original image data before blurring.
Plotted on top of the red line is the traverse from the blurred image
(bottom, green line). The green line shows that a lot of the original
image detail has been lost. For each set above the bottom set are the
processing to try and restore the original image detail or surpass it.
The blue line (2nd from bottom) shows the results from the unsharp mask
(blue line). A small amount of contrast has been restored. The feature
marked by the gray arrow and labeled "A" is discussed in the text.
The results from smart sharpen (cyan line) shows a little more contrast
in the fine detail, but just a little more than the unsharp mask results.
The top set shows the Richardson-Lucy (RL) deconvolution results (black line).
The RL results equal or surpass the original image detail in some
places, but have not matched it in others (e.g. around pixel 22). The RL results, however, show
significantly more detail than either unsharp mask or smart sharpen.
Offsets: blurred image (green + red lines): -15000, unsharp mask: no offset,
smart sharpen: +15,000, RL: +30,000.
The traverses from the images compared to the original image (Figure 6) show that while unsharp mask and smart sharpen enhances local contrast (edge contrast) but do not improve resolution. This is particularly apparent around pixel 4 to 8 in the traverse. Note the gray arrows labeled with the letter A. The unsharp mask (blue) and smart sharpen (cyan) traverse lines are larger at the base of the large peak at pixel 7 to 8 than the original blurred image (green line). So while unsharp mask and smart sharpen has increased accutance, the sizes of some detail has grown larger than the starting image, thus reducing resolution. The Richardson-Lucy deconvolution traverse (black line) has not only improved accutance, the sizes of detail has become much smaller than in the blurred image, increasing resolution over the blurred image by about 2 times.
Down Sampling
There is a myth that it is best to down sample first then sharpen. The images in Figure 6 show examples of before and after sharpening. In each case (Figure C-F), sharpening before down sampling produces a better result, including sharpening both before and after down sampling than no sharpening before down sampling. The myth is busted.
Figure 7. Examples in downsizing. These images are down sampled
by half those in Figures 1-5. Image A was made from the blurred
image from Figures 1, 2, 3, right panel without any before or post
resizing sharpening. Image B is image A then unsharp mask applied only
after downsizing. Images C-F all started with a sharpened images before
downsizing, and ALL those pre-sharpened images show sharper results after
downsizing, even when no additional sharpening is applied after downsizing
(e.g. image D). Images D, E and F started with the RL restored images
from Figures 3, 4 right panel, then downsized.
Anyone is welcome to take the original blurred image in my first post in the series and down sample by 2x and then sharpen to try and produce a sharper result than I show in Figure 7 (e.g. images E or F). The 16-bit tiff (778 Kbyte) blurred image is here: crowned.cranec02.25.2011.C45I7154.ps.b-bin3x3-gaussblur1.0c1.tif and you may download it and manipulate it for non commercial uses. Let me know your results if you produce a sharper down sampled image.
Conclusions and Discussion
The examples shown here demonstrate that image deconvolution produces much sharper results than unsharp mask or smart sharpen. Over the last few years I have used Richardson-Lucy image deconvolution on many of my images, including many displayed on this web site. In my experience, I can improve resolution about 2x on high signal-to-noise ratio images. This means that with a 16 megapixel image, I can produce a sharp higher resolution image equivalent to a 64 megapixel camera.
However, as signal-to-noise ratio drops, it is more difficult to improve resolution without enhancing noise which may already be high. Thus, image deconvolution improvements are less.
Image deconvolution iterations reach a plateau and then only seem to enhance noise. In my experience it is best to find that plateau and stop the iterations just as the plateau is reached. Then run unsharp mask or smart sharpen on that result and try additional image deconvolution iterations using a smaller point spread function. A final unsharp mask on that result can help perceived sharpness. The multiple combinations of image deconvolution and unsharp mask (edge contrast enhancement) produces the best results in my experience with hundreds of images.
Often there is not one blur size in an image, especially considering depth of field issues. Thus, I run the above image deconvolution, edge contrast enhancement, image deconvolution sequence with different point spread functions to optimize the results from different parts of the image. I then stack the results in layers in a photo editor and let show through the areas of the restoration that were best modeled with the different runs. Also, the original high signal-to-noise ratio background that does not need sharpening is kept, so that the only portions of the deconvolved image that show are those portions that need sharpening. It is this combination that produces the sharpest images, containing the most detail with the smoothest backgrounds.
I produce my highest resolution images and sharpen them to the best level before I consider down sizing for prints or web. After downsizing, I run a second level of sharpening. The idea to only sharpen after downsizing is a myth.
This is part 2 of illustrating image sharpening methods. Next: part 3 is here: http://www.clarkvision.com/articles/image-restoration3/.
Image Sharpening Introduction: http://www.clarkvision.com/articles/image-sharpening-intro/
Part 1 is here: http://www.clarkvision.com/articles/image-restoration1/
Part 2 is here: http://www.clarkvision.com/articles/image-restoration2/
Part 3 is here: http://www.clarkvision.com/articles/image-restoration3/.
Image Processing Software with Richardson-Lucy Deconvolution
MLUnsold Digital Imaging: Images Plus: http://www.mlunsold.com Note: the above examples on this web page used ImagesPlus
RawTherapee (free, open source and runs on Linux, Macs and Windows.) (Note, It took about 30 seconds on Linux mint, from the idea to completing the install of RawTherapee: Click to open synaptic package, type in RawTherapee in the search window, click on the RawTherapee line, mark for install, and click apply. In about 5 seconds it was installed.)
PixInsight Commercial image processing software. (I have not used this software. It runs on Linux, Unix (FreeBSD), Macs and Windows.)
Related References:
Image Restoration http://www.astrosurf.com/re/resto.html
Image Deconvolution References:
Bracewell, R.N. "The Fourier Transform and its Applications", McGraw-Hill Electrical and Electronic Engineering Series. McGraw-Hill, 1978.
Cornwell, T. and Alan Bridle, "Deconvolution Tutorial", NRAO, 1996. (http://www.cv.nrao.edu/~abridle/deconvol/deconvol.html)
Goodman, J., "Introduction to Fourier Optics", McGraw Hill, 1996.
Hanisch, R.J., and R.L. White (ed.), "The Restoration of HST Images & Spectra II", STScI, 1993.
Lucy, L.B., "An iterative technique for the rectification of observed distributions", Astronomical J., 79, 745, (1974).
Peyman Milanfar, "A Tutorial on Image Restoration", CfAO Summer School 2003. (http://cfao.ucolick.org/pubs/presentations/aosummer03/Milanfar.pdf)
Richardson, W.H., "Bayesian-Based Iterative Method of Image Restoration", J. Optical Society America, 62, 55, (1972).
Roggemann, M. and B. Welch, "Imaging Through Turbulence", CRC Press, 1996.
Starck, J.L., et al., "Deconvolution in Astronomy: A Review", Pub. Astron. Society Pacific, 114, 1051-1069, 2002.
Blind Deconvolution (need to solve for both the subject and the point spread function): Key References:
Ayers & Dainty, "Iterative blind deconvolution and its applications" , Optics Letters 13 , 547-549, 1988.
Conan et al., "Myopic deconvolution of adaptive optics images by use of object and point-spread function power spectra", Applied Optics, 37, 4614-4622, 1998 .
Holmes , "Blind deconvolution of speckle images quantum-limited incoherent imagery: maximum-likelihood approach" , J. Optical Society America A, 9, 1052-106, 1992.
Jefferies and Christou, "Restoration of astronomical images by iterative blind deconvolution" , Astrophys. J. 415, 862-874, 1993.
Lane , "Blind deconvolution of speckle images" , J. Optical Society America A, 9 , 1508-1514, 1992 .
Schultz , "Multiframe blind deconvolution of astronomical images" , J. Optical Society America A, 10 , 1064-1073, 1993.
Thiebaut and Conan, "Strict a priori constraints for maximum-likelihood blind deconvolution" , J. Optical Society America A, 12 , 485-492, 1995.
Deconvolution from Wavefront Sensing
Primot et al. “Deconvolution from wavefront sensing: a new technique for compensating turbulence-degraded images" , J. Optical Society America A, 7, 1598-1608, 1990.
Notes:
DN is "Data Number." That is the number in the file for each pixel. I'm quoting the luminance level (although red, green and blue are almost the same in the cases I cited).
16-bit signed integer: -32768 to +32767
16-bit unsigned integer: 0 to 65535
Photoshop uses signed integers, but the 16-bit tiff is unsigned integer (correctly read by ImagesPlus).
| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
http://www.clarkvision.com/articles/image-restoration2
First Published January 12, 2014.
Last updated January 12, 2014