
Telephoto Reach, Part 2:
Telephoto + Camera System Performance
(A Omega Product, or Etendue)
(Advanced Concepts)
by Roger N. Clark
All images, text and data on this site are copyrighted.
They may not be used except by written permission from Roger N. Clark.
All rights reserved.
Introduction
Some photography, including birds, general wildlife photography, sports and other
photography of action at a distance, as well as astrophotography requires
resolving small details while having enough signal-to-noise to produce
a quality image. This becomes difficult when the action is fast requiring
short exposure times (e.g. wildlife action, especially near sunrise or sunset),
or when the signal is extremely faint, as in astrophotography.
Many photographers, especially beginning wildlife photographers seem most concerned
with focal length. But aperture is equally important. The lens collects the
light, the focal length spreads out the light, and the pixel chops up the
light into small details to make up the image. The larger the diameter the lens,
to more light it collects. The longer the focal length, the more the light is
spread out over the pixels, and different sized pixels will collect different amounts
of light from a given lens. Adding a teleconverter (TC) increases the focal length,
so spreads the light out more, potentially resolving more detail, but the light
gathered by the lens is not increased, so signal per pixel decreases, along with
signal-to-noise ratio. It is the drop in signal-to-noise ratio that people
perceive as increased noise in an image. Similarly, if the pixel size is
decreased, the light per pixel is decreased while resolution is potentially
increased. But again the total light collected by the lens has not changed,
to signal-to-noise ratio decreases. In fact there is little difference
between adding a TC and decreasing pixel size.
The above properties are well known in scientific remote sensing
applications (e.g. aircraft and spacecraft sensors) and well described by
basic physics. These properties also apply to wildlife, sports, and
other photography requiring lenses (or telescopes) where
exposure time is limited (e.g. a short exposure time is needed to
prevent blur due to subject movement). These principles include
wildlife action photography with telephoto lenses, and even
astrophotography with a telephoto or wide angle lens, or with a telescope.
Executive Summary
A significant conclusion is that for telephoto reach, smaller pixels
are better than a camera with larger pixels with the use of TCs, all
else being equal. Telephoto reach is more than simply focal length;
it is lens diameter, and focal length coupled with pixel size.
The A Omega Product (Etendue)
The Etendue of a system determines fundamental performance of the lens
plus camera, so bear with me while I try and describe it. There are also
several non-intuitive results (at least for most photographers) that come out
this concept which should help photographers choose and understand
the performance of different lenses and cameras. This knowledge should lead to
better choices. For example, should one choose a used Canon 1D Mark III
camera or a newer 7D camera to give the best performance for bird
photography? (We define best performance as giving the most pixels
on the subject with actual resolved detail and highest signal-to-noise
ratio.)
Another example, I have a 300 mm f/4 lens, but I want more telephoto
reach. I can't afford a 500 mm f/4 lens, but will a 300 mm f/2.8
really be much better than my 300 f/4? After all, both lenses have
the same focal length. We shall see, however, that the increase in
aperture makes a big performance increase, so yes, the move up to the
larger lens will be a significant improvement assuming quality lenses.
The basic formula for Etendue can take several forms (see
references), but comes down to the diameter of the lens (or telescope)
collecting the light, and how finely that light is separated in the focal
plane to form the pixels in an image. It matters little if the light
in the focal plane is sampled by many tiny pixels by a short focal lens,
or larger pixels fed by a longer focal length lens. What matters is the
size of the detail on the subject that is projected into the focal plane,
sampled by the pixels, and how much light is delivered to each pixel.
The basic physics says to use the largest diameter lens to obtain the
highest signal-to-noise ratio, and the combination of focal length and
pixel size to resolve the desired detail.
For example, let's say we have a lens that collects 1,000,000 photons on a subject
and we have 10,000 pixels. That leaves us with 1,000,000/10,000 = 100 photons per pixel.
If we want finer detail, we can make the pixels smaller, for example,
by cramming 20,000 pixels into the same sensor area, but then we have
less light per pixel: 50 photons per pixel in this example. It is like
feeding people pieces of pie. Our pie is only so big, so to feed more
people, each must get a smaller piece of pie. The alternative is to buy
a larger pie. Some may think the larger (photographic) pie in this situation
is a larger sensor, but a larger sensor dose not collect more light over a given
amount of detail. Only a larger lens can collect and deliver more light.
So in photography, the more pie analogy is a larger diameter lens. This is
the basic reason why an f/2.8 lens of a given focal length will deliver
more light to the sensor than an f/4 lens of the same focal length over a given
time interval (exposure time).
In telephoto photography, another factor, besides lens quality is diffraction.
Diffraction limits detail in an image. One can boost focal length (e.g. add
a teleconverter, TC, or buy a longer focal length lens of the same aperture diameter)
but ultimately, detail is limited by diffraction. With today's digital cameras,
diffraction plays a significant role at f/ratios of f/8 and even smaller with
small sized pixels. Diffraction effects were covered in part 1 and are included
in the calculations here (see:
Telephoto Reach and Digital Cameras, Part 1.
An example: one has a 300 mm f/4, would imaging results
be much better with 400 mm f/5.6 assuming both are top quality lenses?
The answer is no. The 300 mm f/4 has an aperture of 300/4 = 75 mm and the
400 f/5.6 has an aperture of 71.4 mm. If both lenses were diffraction limited,
the 400 f/5.6 lens would have slightly worse performance.
The two factors that are the fundamental metrics in system performance
are the lens collecting area (A), and the angular size of a pixel
(omega). The collecting area is simply proportional to the square of
the diameter of the lens (technically, the lens entrance pupil).
The signal-to-noise ratio is proportional to the square root of the collecting area,
so is proportional to the lens diameter. These concepts are illustrated in
Figure 1.
The angular size of a pixel (omega) is proportional to the focal
length of the lens and the pixel size. The longer the focal length,
the smaller the angular size of a pixel. Similarly, for a given focal
length a smaller pixel will see a smaller angular size. The angular
pixel size also determines the number of pixels on the subject, and thus
the fundamental limit to the detail that can be recorded. The amount of
light collected by the pixel is proportional to the pixel area, so omega squared.
For this study I use square
arc-seconds. The actual detail resolved is dependent on diffraction
and other lens aberrations. The A*omega factor (proportional to lens
area times linear pixel size squared divided by focal length) gives the
relative signal delivered to each pixel and the signal-to-noise ratio
is proportional to the square root of the A*Omega product.
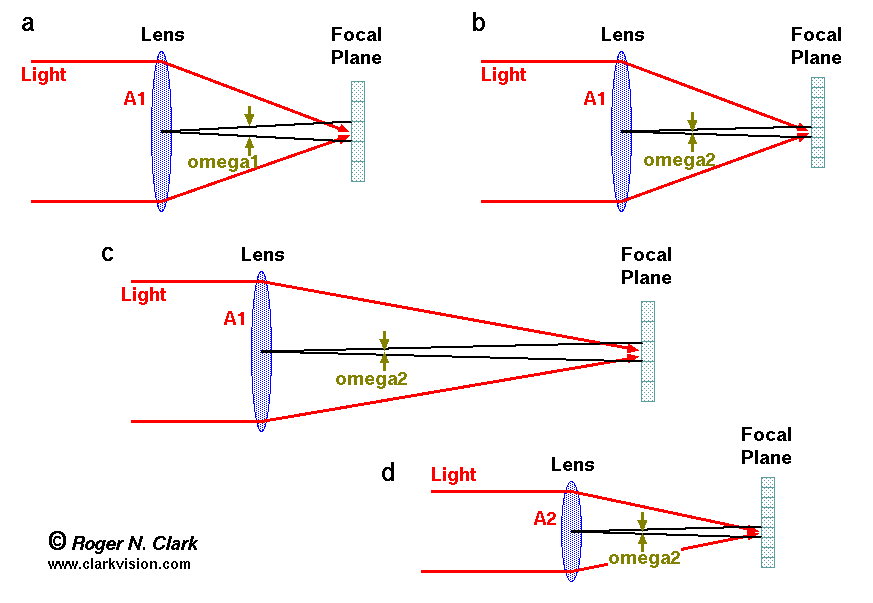
Figure 1. Illustration of the A*Omega concepts. The area of the lens
is A1 in panels a, b, c, and A2 in panel d. The angular size of a pixel,
omega, is also the angular size of the smallest possible detail in an
image (if the lens can deliver that detail) and is omega1 in
panel a, and omega2 in panels b, c and d. In this illustration,
omega2 is half the angular size of omega1. The area of the lens
in panel d (A2) is 1/4 the area of the lenses in panels a, b, and
c (A1). The light per pixel in panel b is half that of panel a.
The angular size of a pixel is the 2-dimensional size, measured in
steradians, square degrees, square arc-minutes, or square arc-seconds/
See text.
The angular size of a pixel also determines the pixels or detail we
can get on a given subject. We define this detail as the lens + camera
acuity. The acuity is defined as the inverse of the angular linear pixel size,
and pixel size in arc-seconds is used here. There are 3600 arc-seconds in
one degree; the Moon appears about 1800 arc-seconds across. The human
eye resolves detail down to about 30 arc-seconds in bright light. As we shall see,
it is difficult to resolve detail smaller than about 1 arc-second with
today's DSLRs and available telephoto lenses (that 1 arc-second metric
can be surpassed with large amateur telescopes).
In the following discussions, the lenses are assumed to be perfect,
limited only by diffraction. All lenses are assumed to have the
same transmittance. The latest super telephoto lenses come close
to diffraction limited performance.
Figure 1 illustrates these properties. The lens in panel a of
Figure 1 delivers A1 light to each pixel with resolution omega1.
In panel b the pixel size is half that in panel a so the light
per pixel drops by 4. Thus, the image in panel b has twice the
pixels on a subject (assuming the subject is small in the frame,
and we measure linearly) but the image is noisier. In panel c,
the camera has the same pixel size as that in panel a, but the
lens focal length is double. Thus the detail is the same as in
panel b with the same noise per pixel. Panel d has the same
focal length lens and the same pixel size as in panel b so the images
have the same pixels on subject. But the lens in panel d is half
the diameter so the light delivered to each pixel is 4 times less
in a given exposure. Therefore the system in panel d has
a signal-to-noise ratio half that in panel b. Focal length,
lens diameter and pixel size all play significant roles in
system performance and image quality. Next we will explore
performance of common lenses and pixels found in today's photography
market.
Figure 2 shows basic trends for 7 lenses and pixel sizes representative
of the cameras available today and the last few years.
The trend lines (see the figure caption) indicate that if one
trades pixel size or adds TCs, one can gain acuity, but
lose signal-to-noise ratio in a given exposure time.
Note, changing ISO does not change a camera's sensitivity. Changing ISO
tells the camera's metering system to change exposure time, and make
a corresponding change in signal gain after the signal is read from
the sensor. So as one increases ISO, the computer reduces exposure
time and increases gain, essentially telling the camera to digitize
a smaller signal range.
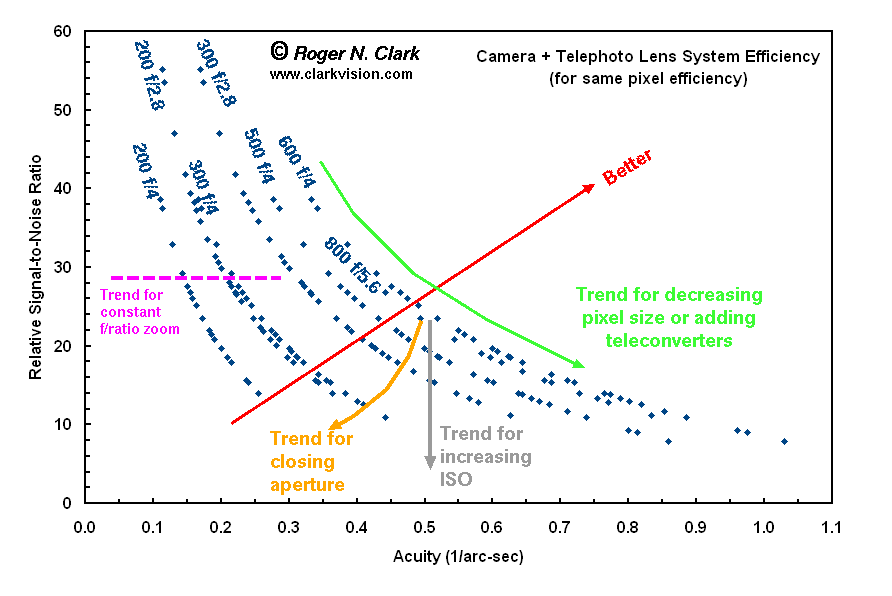
Figure 2. Camera + telephoto lens system performance for 7 lenses and
numerous cameras (assuming all pixels have the same efficiency). Ideally,
one would want top performance in both signal-to-noise ratio and resolved
detail (acuity). Performance following the red line would be ideal,
or a horizontal line near the top of the plot.
A constant f/ratio zoom lens follows the trend of the dotted magenta line
although none reach more than just below the 300 f/2.8 points and consumer
zooms are well short of that mark. The points for a given lens (trends from
upper left to lower right) indicate that performance, whether bare lens,
lens plus TCs, and for cameras with various pixel sizes, ranging from 8.4
microns down to 4.3 microns all follow the same trend. For a given lens
(e.g. the 600 f/4, adding TCs or putting the lens on a different camera
body with smaller pixels produces similar results: the trend follows the
green line. In fact, if the pixels have the same relative efficiency, one
could not tell the difference between adding a TC and reducing pixel size.
Increasing pixel efficiency would shift the points vertically; similarly,
older cameras with lower pixel efficiency would shift the points for a
given lens down (see Figures 3 and 4).
Closing the aperture on a lens reduces light and acuity, following
a curving trend illustrated by the orange line. Increasing ISO does not
change sensor efficiency; it only serves to decrease exposure time
thus reducing signal-to-noise ratio (trend in the gray line).
Figure 2 shows a lot of complexity so let's limit the parameters to
3 cameras and 3 lenses (Figure 3). Again, we assume all three cameras
have pixels with the same efficiency. Given the choice of buying an
expensive pro-level camera (camera A) versus a consumer level camera
(camera C), which would give better performance. The prevailing view
on the net is that cameras with smaller pixels produce noisier images.
But that is not the whole story. To get the same detail on a subject with
camera A as with the smaller pixels of camera C, one would need to add
a 2X TC to camera A. But when one does that the signal-to-noise ratio
drops to that of camera C. Both cameras produce similar images with
almost the same detail on subject with nearly the same apparent noise
(signal-to-noise ratio).
But there are more implications to the above example. Camera C
is producing the detail on subject with the same signal-to-noise
ratio as camera A, but camera C is doing it without teleconverters.
Teleconverters slow down the autofocus (AF) system, so camera C would have
better fast action AF performance (assuming the AF systems were similar
in both cameras). It is also likely that the TCs are not perfect and
there is additional degradation of the image quality beyond diffraction.
A significant conclusion is that for telephoto reach, smaller pixels
are better than a camera with larger pixels with the use of TCs.
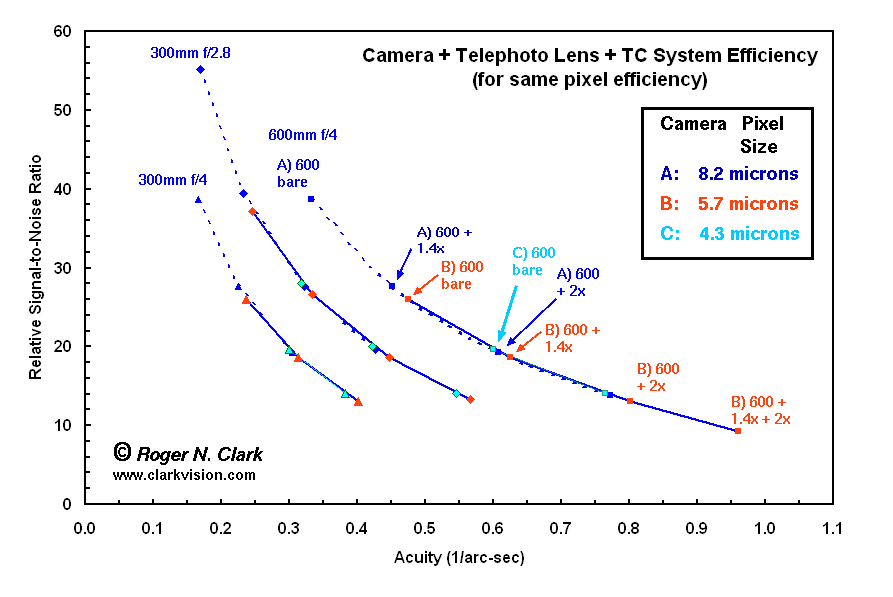
Figure 3. Data from Figure 2 but limited to 3 cameras and 3 lenses.
For each camera, points along the trend represent adding TCs. Cameras A
and B are assumed to be like Canon 1D series cameras and will autofocus
at f/8 and even with stacked 1.4x and 2x TCs, while camera C is like a
consumer camera so will only focus up to f/5.6. Note the ratio of pixel
sizes to cameras B and C is (5.7/4.3 =) 1.33 so adding a 1.4x TC to camera
B produces similar performance as camera C with no TC for a given lens.
Also note camera C produces similar performance as camera A with a 2X TC
(note that diffraction is limiting performance).
Now let's consider pixel efficiency. Pixel efficiency has been derived
for some cameras (see: Digital Sensor Performance Summary, Figure __).
We examine 3 cameras and include their relative pixel efficiency: a
Canon 1D Mark III (7.2 micron pixels), and newer generation 1D Mark IV
(5.7 micron pixels) and 7D (4.3 micron pixels). The results for these
three cameras and for 3 lenses are shown in Figure 4. Now we see that
even though the 1DIII has larger pixels, the pixels have lower collection
efficiency so plot lower in terms of relative signal-to-noise ratio.
The results show that the 1DIV with a 1.4x TC produces slightly more detail
(higher acuity) than a 7D camera with no TC when using the same lens.
The 1D Mark III needs a 2x TC to beat the acuity of the 7D or 1DIV+1.4x
TC but has much lower signal-to-noise ratio. The 2X TC would also
significantly slow down AF performance.
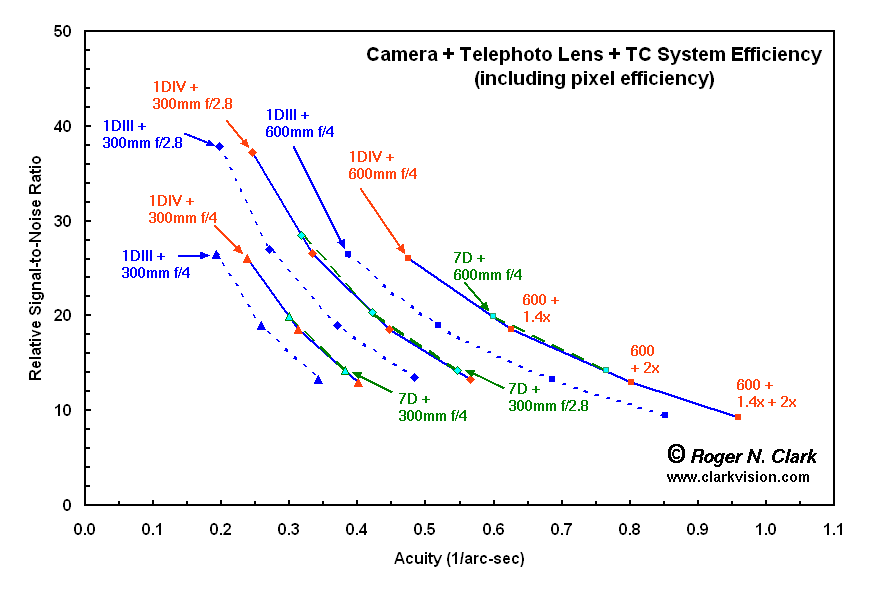
Figure 4. Lens + camera performance for 3 cameras and 3 lenses.
The 1D Mark III has lower pixel efficiency than the newer generation
cameras: the Canon 1D Mark IV and 7D. Thus the data points for the
1DIII are shifted vertically down from the trend in Figure 2.
Next let's compare lenses on the same camera (Figure 5). How does
performance improve going from a 300 f/4 to 300 f/2.8 to 500 f/4 to 600
f/4 lenses? If we start with a 300 f/4, like many beginning wildlife
photographers do, the acuity is limited and many photographers want more
reach. The 300 f/2.8 can give wonderful shallow depth-of-field, but when
TCs are added, focal length is substantial and a large boost in acuity.
The 300 f/4 with a 2x TC is f/8 (so will not autofocus on consumer
cameras but will on the pro series) and the about 0.4 with a relative
S/N of about 13 in Figure 5. However, the 300 f/2.8 with a 2x TC is at
f/5.6 (so will autofocus on consumer cameras), the acuity is higher at
about 0.45, while delivering better S/N (18 in figure 5). Further, the
autofocus performance is fast at f/5.6 than at f/8, giving another edge
to the 300 f/2.8 lens. Thus, if one cannot afford a 500 or 600 mm lens,
the 300 f/2.8 is still a significant leap in performance over the 300 f/4.
Diffraction affects acuity of smaller aperture lenses. For example, compare
the 300 f/2.8 + 2x TC point (follow the 300 f/2.8 trend down two points
to the f/5.6 line) with the 600 mm f/4 bare. The 600 mm f/4 lens has an acuity
of about 0.5, whereas the 300 + 2x TC = 600 mm f/5.6 has an acuity of
about 0.45. The loss in acuity is due to diffraction from the smaller aperture.
Aperture plays a key limiting role in the ability of a lens to resolve
fine detail. Not only does the larger diameter lens deliver more light,
but diffraction effects are less, improving resolution of fine
detail and improved contrast in fine details. This of course assumes
equally high quality among the various lenses.
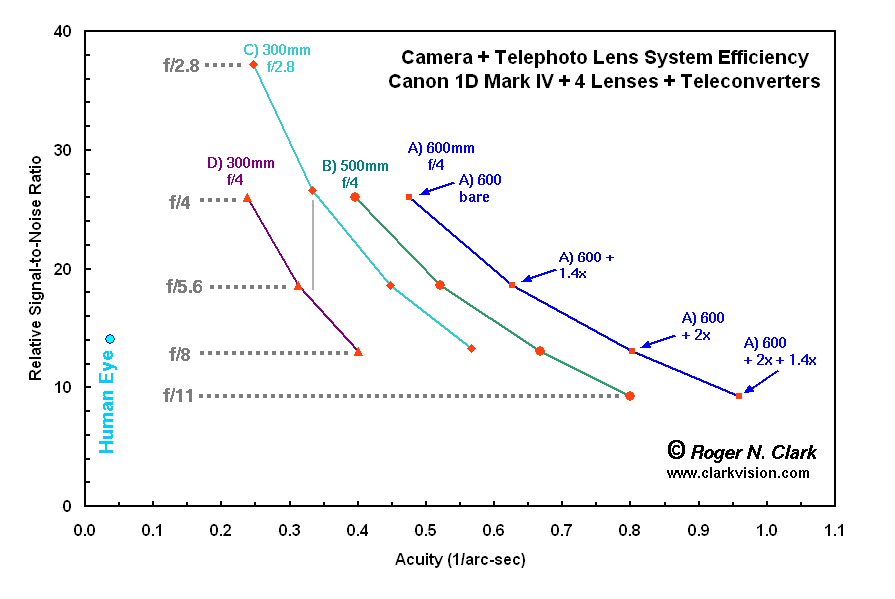
Figure 5. The system performance of four lenses are compared with one camera.
Constant f/ratios are horizontal lines (the dashed gray lines). The small
vertical gray line between the 300 f/4 and 300 f/2.8 trends shows that at the
same focal length the 300 f/4 lens falls short of the acuity of the
300 f/2.8 lens due to increased diffraction from the smaller aperture
diameter. The human eye point is for the comparison of the acuity only;
the signal-to-noise position is arbitrary.
So far we've discussed the trends assuming a constant wide open aperture.
What happens if one closes down the aperture diaphragm is shown for two
cameras in Figure 6. For cameras with larger pixels, stopping down
has minimal effects up to about f/8, but diffraction effects become larger
at smaller apertures (larger f/ratio numbers). Cameras with smaller
pixels show the diffraction effects at larger apertures.
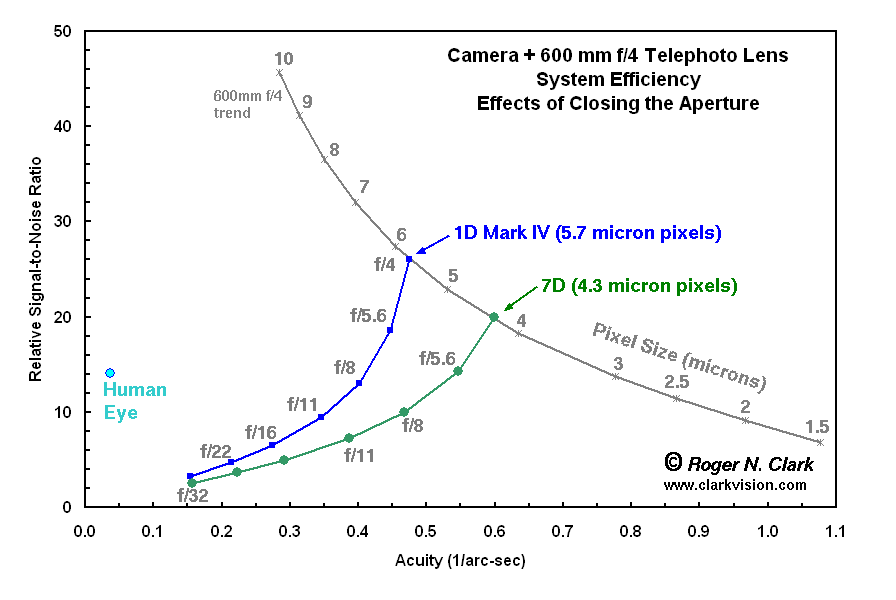
Figure 6. Effects of system performance when reducing the aperture
diameter on a 600 mm f/4 telephoto lens for two cameras. There is a loss
in light due to the smaller aperture and in acuity due to diffraction.
The camera with smaller pixels shows the effects more but the acuity
remains higher and the S/N remains lower.
Often photographers are faced with low light and needing to boost ISO
to maintain a fast enough exposure time to prevent blur due to action
in the scene or camera shake. The effects of ISO are illustrated in Figure
7. Digital camera sensors have only one sensitivity. Changing ISO only
tells the camera to expose for a shorter period and boost the signal
more than at lower ISOs. Thus, as one boosts ISO to shorten exposure,
S/N drops with the square root of the relative increase in ISO.
Acuity is not affects unless noise becomes very low then noise can
mask fine detail. Thus, it is better to keep ISO low if exposure times
are fast enough to prevent blur (unless of course one is trying to
make artistically blurred images).
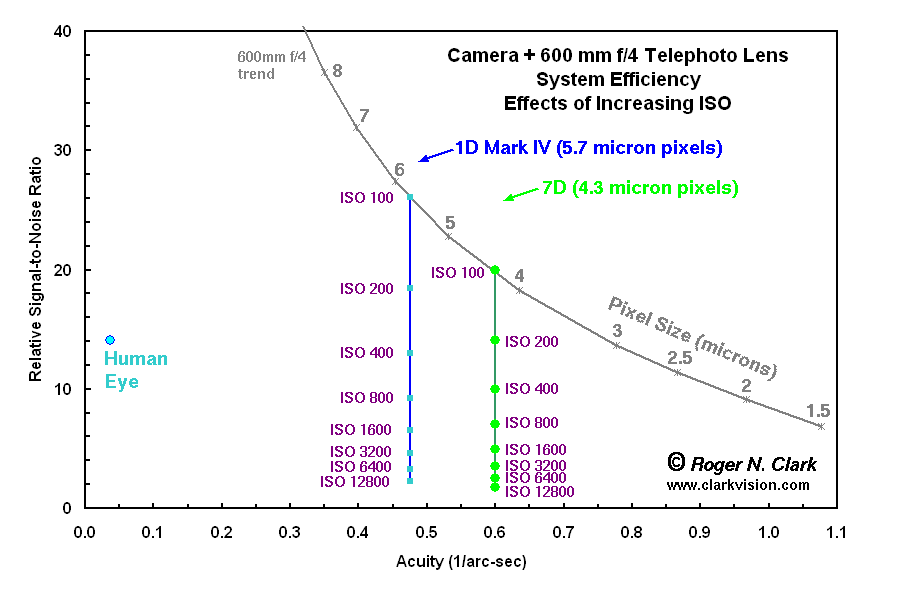
Figure 7. Effects of ISO. ISO does not change sensitivity of the sensor;
it only shortens exposure time limiting the amount of light that
the sensor can capture.
Here is a demonstration of the effects described in the above post on
Etendue. Three cameras, with pixels sizes ranging by almost a factor of
2, same lens, same exposure time, same ISO (1600), same lens aperture
diameter. Can you tell what the cameras are? I'll give the answers,
but a hint: they are mentioned above. Another hint. The signal-to-noise
ratios on a 16x16 pixel block on the gray patch below the 1 in "1px" are
(in no particular order): 8.4, 10.5, 11,8, again in the order I would
predict. Which camera has the highest S/N, and which has the lowest? The
images are from the raw data, converted with the same settings in ACR,
then a very small white balance correction (less than 1%) applied in
photoshop. Statistics on 16-bit data, Adobe RGB. Presented here, of
course is 8-bit sRGB jpeg.

Figure 8. comparison
Here are the detail on the comparison. Left: 7D + 500 mm lens at
f/4. Center: 1D4 + 500 mm + 1.4x TC at f/5.6, Right: 1D2 + 500 mm + 2x TC
at f/8. So the 7D image has the highest S/N, the 1D4 next and the 1D2 is
the lowest. But there is a slight bias. The 7D pixels are 4.3 microns,
and 1D4 are 5.7 microns, for a ratio of 1.33. As we only have 1.4x TCs,
the 1D4 image size (pixels on subject) is 5.2% more magnification so 5.2%
more pixels on subject. But that also means the signal is lower by 1.052
squared, so the S/N on the 7D would be 5.2% higher. I measured the S/N
of the 7D (on the gray patch noted above) to be 11.8, the 1D4 S/N = 10.5
and the 1D2 S/N = 8.4. Thus, the 7D came out 12% higher. But the measured
efficiency of the 7D is about 6% higher than the 1D4 (see Figure 10 at:
Digital Camera Sensor Performance Summary).
Thus with 5% and 6% more efficiency we should have seen a ratio of 7d
to 1D4 S/N's of 11% amd we measured 12%, which is impressively close!
Now the 1D4 to 1D2 pixel ratios is 8.2/5.7 = 1.44, so the jump from
1.4x on the 500 with the 1D4 to the 2x on the 1d2 is virtually a perfect
match. If the 1D2 were the same pixel efficiency as the 1D4, the images
would be identical (assuming no loss from the 2x TC). But the 1D2 pixel
are less efficient by over a factor of 2 (see Figure 10 referenced above),
so the S/N on the 1D4 should be higher by about 1.45x but it measured as
10.5/8.4 = 1.25, so the 1D2 came out 16% better than expected, which is
still very close. My 1D2, deing quite old with a lot of shutter actuations
shows a little variation from exposure to exposure so the difference is
likely due to variation in shutter speed. Note this is only 0.2 stop.
So the results of the test are very close to predicted and well explained
by Etendue. Equalizing the cameras, especially 1D4 and 7D produces nearly
identical images. But wait, the 1D4 image looks a little better than
the 7D image. That is because the focal length is slightly greater so
slightly better resolves the detail. It someone has a 1.3x TC, we could
make the images look even closer.
The bottom line for photographers is the 7D is not a noisy camera compared
to other cameras. it is all in how it is used. 1D series cameras have
many advantages but not in lower noise when one equalizes pixels on
subject and exposure time with the same lens. If I couldn't afford a 1D
series in the canon line, I would choose the 7D for bird photography. The
same principles apply to all other cameras, especially those made in
the same generation. Smaller pixels give more pixels on subject with
a shorter focal length lens, and larger pixels do not have an advantage
concerning noise.
Another factor: f/8 AF is slower. If one needs 2X TCs and f/8 a lot,
it would probably be better to get a camera with smaller pixels and work
at f/5.6 for the faster AF.
Other Ways to Look at the Problem
An up and coming myth is the very misunderstood big pixels are less noisy idea.
A larger pixel enables the collection of more light, not that they collect
more light. Consider this analogy: You have two buckets, one that holds
2 gallons of water and one that holds 1 gallon of water. You put the
2-gallon bucket under the faucet and turn on the water for 1 second. Now
you put the 1 gallon bucket under the faucet and turn on the water at the
same intensity for one second. Assume the amount of water was not enough
to overfill either bucket. Which bucket has more water? (If you answer I
hate story problems you fail the class.) If your answer is both buckets
have the same amount of water, you are correct. Now what controls how
much water is in the bucket? It is not the size of the bucket; it is
the force and duration of the water controlled by the faucet.
In digital photography, the bucket is the pixel, the faucet is the lens
and the time the faucet is on is the exposure time. There is one thing
missing in the analogy, and that is focal length which spreads out the
light so if the faucet has a spray nozzle on the end the spray would
expand a further distance from the faucet. Now for the larger bucket,
if it has a larger diameter, it would collect more water because it
sees a larger area. But if the smaller bucket were moved closer to the
sprayer, so it collected the same angular area, it would also collect the
same amount of water. People talk about the same sensor field of view,
but there is also the same pixel field of view. When the pixel field of
view is the same, regardless of pixel size, the two pixels collect the
same amount of light in the same amount of time and produce the same
signal-to-noise ratio.
So in the case of digital cameras, the amount of light collected is
controlled by the lens, its focal length and the exposure time. The larger
pixels only ENABLE the collection of more light when the exposure time
is long enough. With digital cameras, that only happens at the lowest
ISO. At higher ISO, the buckets (pixels) never get filled.
So to manage noise in digital camera images, one must manage the lens
aperture, the focal length, and the exposure time. The focal length
manages the pixel field of view. So it is not the pixel that controls
the observed noise in an image.
Conclusions
Both aperture and focal length are important in producing fine detail on
a subject with good signal-to-noise ratios. Adding TCs reduces light to
each pixel by spreading the light out, and the reduction of light
to each pixel is the same as reducing pixel size. For comparisons of different
camera + lenses, in terms of noise, there is no difference between adding
TCs or reducing pixel size. Smaller pixels do not inherently produce
noisier images because there is a continuum trade between acuity and
signal-to-noise ratio, whether by increasing focal length or decreasing
pixel size.
One can trade high signal-to-noise ratio for detail on a subject.
For example. in low light situations, use a shorter focal length lens
(e.g. 300 f/2.8 instead of 300 f/2.8 + 1.4x TC).
To collect more photons in a single pixel, at least one of these conditions
must hold: 1) larger diameter lens, 2) shorter focal length for the same diameter
lens, and/or 3) larger pixel. For example, a larger
bucket in a rain storm is needed to collect more
water. But while the pixel collects the light, it is the lens that
delivers the light, and the larger the diameter of the lens, the more
light you pump to the pixel. The larger pixel simply enables more light
to be collected without overflowing.
Cameras with larger pixels are NOT inherently less noisy. The larger pixels
only enable more light to be collected to produce higher signal-to-noise ratio images.
But it is the lens and exposure time that deliver the light to the pixels.
Larger pixels = less detail. It is a continuum trade between detail and
light per pixel. There is no free lunch. If you want the same detail
on a subject as a camera with smaller pixels, and you increase focal length
to get that detail, you won't have higher signal-to-noise ratio images just
because your camera has larger pixels. With the same detail and same lens
diameter, you'll get the same signal-to-noise ratio per pixel regardless
of pixel size for a given exposure time.
No free lunch and no magic large pixels.
Lens aperture is equally important to focal length in overall system
performance. Buy the largest aperture lens you can afford and that you
have the ability to carry.
Additional Reading
Telephoto Reach and Digital Cameras, Part 1
Pixel Size, ISO and Noise in Digital Cameras
http://www.newport.com/Tutorial-Light-Collection-and-Systems-Throughput/381845/1033/content.aspx
http://en.wikipedia.org/wiki/Etendue
Crop Factor and Digital Cameras
Digital Cameras: Does Pixel Size Matter?
Factors in Choosing a Digital Camera (Does Sensor Size Matter?)
Good digital cameras are photon noise limited. This sets basic properties
of sensor performance.
The f/ratio Myth and Digital Cameras.
Etendue, or Optical Throughput.
http://clarkvision.com/articles/telephoto.system.performance
First Published March 23, 2012
Last updated May 23, 2017.






