ClarkVision.com
| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
Nightscape Photography with Digital Cameras
(Landscape Astrophotography)
by Roger N. Clark
| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
by Roger N. Clark
Nightscape photography, or photography of the night sky with foreground landscapes, is an exciting new area of photography where digital cameras excel. But there are many misconceptions online and in print about night photography. This series of articles tells the real story and busts many myths as well has giving important information for photographers to make better night images.
The Night Photography Series:
Contents
Introduction
Nightscape and Digital Camera Myths

Nightscapes refers to landscape photography at night, usually including stars or other interesting subjects only visible at night and integrating the land and sky into the recorded scene. Nightscape photography can be done with simple cameras and lenses except for the case where one wants to record stars in the scene without trailing or other cases with moving subjects in a very low light situation. Light from stars in the night sky is very faint and to record those stars relatively quickly before the Earth's rotation blurs the stars into a trail places important constraints on the imaging system.
Unfortunately, as with many aspects of digital photography and the web, there are many misleading web sites with outright wrong information regarding nightscape photography and what is the best technology to use. With this article, I will try and set the record straight.
I have done night photography for over 40 years. A lot of my night imaging is with NASA spacecraft, imaging planets, satellites and faint ring systems. I took my first professional digital night images in 1976. It is through my professional work that I understand how the sensors and electronics in digital cameras work and apply that in my DSLR nightscape and astro photography. You can see some of my work on digital camera sensors at: http://clarkvision.com/articles/digital.sensor.performance.summary/.
Also see my night images gallery: http://clarkvision.com/galleries/gallery.night/.
A significant misconception in night photography (or any photography for that matter) is that ISO changes sensitivity. If you keep exposure time and f/stop on a given lens the same and vary ISO, there is no change in the amount of light the sensor captures. See: http://clarkvision.com/articles/iso/
Pushing up in ISO to high levels only reduces dynamic range; there is no change in sensitivity. ISO is post sensor gain and all one needs to do to is get the gain high enough to amplify the signals from the sensor above the noise from post sensor electronics, including fixed pattern, or banding noise. With the Canon 5D2, that occurs at about ISO 3200. For the 1D4, it is at about ISO 1600. Figure 2 illustrates the effects. At ISOs below 1600 on the 5D2, post sensor electronics noise dominates above sensor read noise (gray band in Figure 2). Above ISO 1600, dynamic range is reduced in proportion to the increase in ISO. With the 5D2, a small amount of banding noise is evident in some images, so I usually use ISO 3200 for nightscapes. At this ISO (amplification) any under exposure can be adjusted in post processing with no added detriment to image quality because the signal and noise from the sensor is digitized adequately.
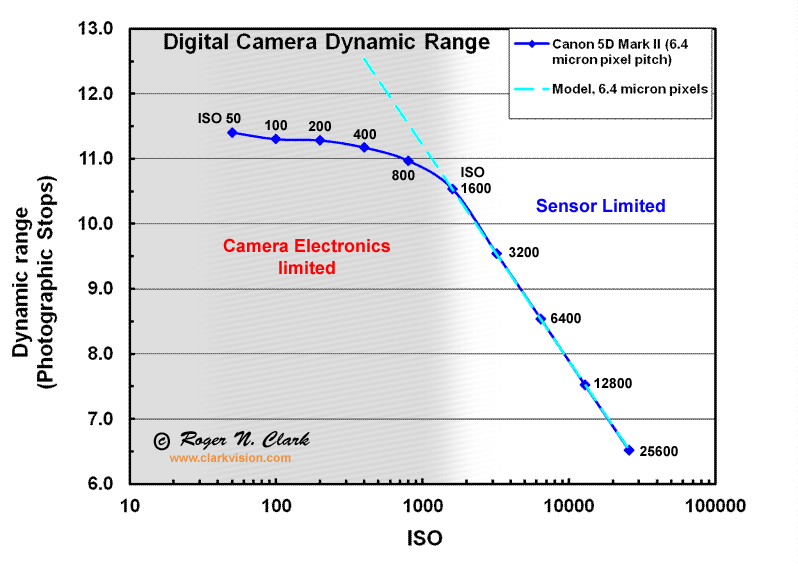
Figure 2. Dynamic range as a function of ISO for a Canon 5D Mark II.
The gray zone represents where the post sensor electronics is
limiting dynamic range and shadow detail. The white zone starting at
about ISO 1600 is the sensor limited zone. There is no point in
increasing ISO above 1600 to 3200 on the 5D Mark II as dynamic range
is dropping. The cyan dashed line is an ideal model response with no
added noise from downstream electronics. The faint banding in the gray
zone represents possible banding noise in images, and the level in the diagram
is 1/5 the intensity of the solid gray, showing that low level
banding can be annoying in images. On my 5D Mark II, I need to
raise ISO to 3200 so that sensor read noise swamps the banding.
ISO does look like sensitivity, but it is more like digital zoom: yes it looks like zoom but you really didn't gain anything. Let's say you are doing 30 second exposures at f/2. As you change ISO above 1600 the data numbers get brighter, the camera LCD gets brighter, but you don't actually record any fainter stars or nebulae. Use of lower ISOs than about 1600 on many camera does not amplify the weak signals enough to get them above downstream electronics noise (Nikon and Sony are exceptions--ISO 800 works well too). If you image at ISO 1600 and 6400, then boost the ISO 1600 image two stops in the raw converter, it will look almost identical to the 6400 ISO image in terms of noise and saturated stars. So all you gain is more saturated stars without any more fainter stars. It is a very simple operational setting in the field to significantly improve ones night images. All cameras behave similarly (Nikons and Sonys keep improving toward lower ISOs unlike Canon's which flatten out at ISOs below about ISO 1600).
It is best to image at the lowest ISO that gets above those noise problems from camera electronics and no higher. That gives the most dynamic range to keep star colors in the brighter stars. ISO 1600 is a good compromise on most cameras. You'll see that I use ISO 1600 for most of my nightscapes and astrophotos.
On the web and in magazine articles, I have read that Point and Shoot cameras are poor for use in nightscape photography because of greatly reduced sensitivity. Then next these articles cite that DSLRs are better because of their larger sensors and larger pixels. Also, that DSLRs with larger pixels are better than DSLRs with smaller pixels. All of this is untrue--another myth!
All digital cameras for general photography in the visible part of the spectrum (what we see with our eyes) use silicon detectors, whether CCD or CMOS technology. This technology has been in use for decades and is quite mature. Sensitivity is defined as the percentage of light that strikes the detector that actually generates a measurable signal, and is called the quantum efficiency (QE). There are two general types of CCD and CMOS technology: 1) standard front side illuminated sensors with a peak quantum efficiency around the 30 to 40% range, and 2) back side illuminated with a peak quantum efficiency in the 90+% range. There are no back side illuminated DSLRs as of this writing, but there are some point and shoot cameras with this technology. Back side illuminated sensors are more difficult to manufacture. But what this means is that the efficiencies of small sensor point and shoot cameras are similar in sensitivity or more than a factor of 2 higher in sensitivity than the sensors in DSLRs, not less as many web sites and magazine articles proclaim!
On my digital sensor performance article (see link above), I show that small pixels collect less light. The analogy is buckets in a rainstorm: smaller buckets will collect less water than a large bucket. But in a pixel array, small pixels get more detail. It is a trade between light per pixel and image detail. It is also true that a larger pixel will collect more light with a given lens in a given exposure time. But how bad is it? The key is that for a given lens, the detail for a given spot size on the sensor is constant, given the same technology. For example, the light from star images on a sensor by a given lens sends the same amount of light to the sensor regardless of the pixel sizes of the sensor. The light recorded by the sensor is basically the same, whether the light is spread over one or a dozen pixels. In theory, if the sensors had the same read noise and same electronics noise, the larger pixel sensor will have a slight advantage, having square root the number of pixel advantage over the small pixel sized sensor in terms of recording fainter stars. But other factors come into play too, including improving technology such as better fill factors, better micro lenses on the sensor, and lower noise. Thus, a better metric to sensitivity is signal per unit area in the focal plane. This is shown in Figure 3, a copy of Figure 10 from the http://clarkvision.com/articles/digital.sensor.performance.summary/ article.
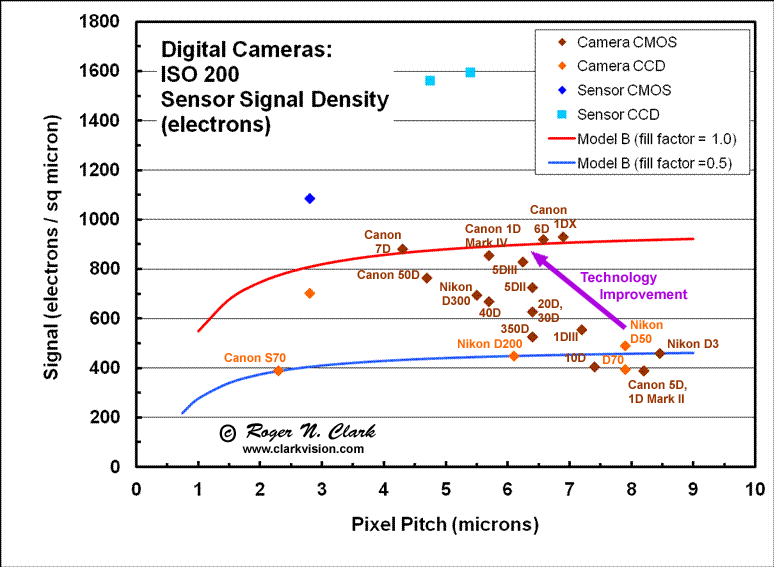
Figure 3.
Sensor signal density. A significant trend in improvement of sensors is
evident in the data from sensors spanning about a decade. Improvements
include better fill factors (the portion of a pixel that is sensitive
to light), better transmission of the filters over the sensor (the red,
green and blue Bayer filters, the infrared blocking filter and the blur
filter. Solid lines are models that show what the trends would be if
technology were constant and pixel size varied. The trend is down with
smaller pixel size because the non-sensitive portion between pixels
becomes a greater part of the pixel area. The models here have 0.25
micron spacing between pixels. Even with gapless microlenses, light will
be lost at the gap due to scattering.
If we compare the Canon 5D Mark II, 1D Mark IV, and 7D, which will come out on top for nightscape photography. If we believe other web sites and magazine articles, the 5D Mark II, with its large pixels should record much fainter stars than the smaller pixel size cameras. Figure 4a and 4b shows the real story. Which camera image shows the faintest stars? It is clear that the 7D shows the most, with the 1D Mark IV a close second, and the 5D Mark II trailing behind. This is exactly what was predicted by the data in Figure 3.

Figure 4a. The stars around the North Star, Polaris, are shown for
three cameras using the same lens at the same ISO, f./ratio, and exposure time.
These images were obtained within a few minutes of each other in the very
dark skies of the Island in the Sky district of Canyonlands National
Park, Utah, USA. These images are cropped and shown at the original out of
camera image size (1 camera pixel = 1 pixel on the screen) and all
images have had the same processing. The slightly
redder background in the 1D Mark IV image is apparently a
change in background airglow and should
not be attributed to the camera.

Figure 4b. The stars around the North Star, Polaris, are shown for
three cameras using the same lens at the same ISO, f./ratio, and exposure time.
These images were obtained within a few minutes of each other in the very
dark skies of the Island in the Sky district of Canyonlands National
Park, Utah, USA. The 5D Mark II and 1D Mark IV images have been
resampled so the images appear the same size as that for the 7D image,
and all images have had the same processing. The slightly
redder background in the 1D Mark IV image is apparently a
change in background airglow and should
not be attributed to the camera.
So why the apparent discrepancy in observed performance between small sensor point and shoot cameras and DSLRs? And why aren't smaller pixels bad as people say?
Now that we've debunked the ISO and pixel size equals higher sensitivity myths, the real story in nightscape system performance is the lens: larger clear aperture lenses collect more light. Astronomers have known this for centuries; that is why they build large telescopes: to gather more light. The key to more light gathering is the clear aperture of the lens, and not the f/ratio as is commonly believed.
Confusion emerged with digital cameras with different sensor sizes. It became evident that small sensor cameras like those typically found in point and shoot cameras produced images with more apparent noise (lower signal-to-noise ratios, or SNR). The lower SNR was erroneously attributed to the smaller sensors. But look what happens with a smaller sensor camera: a shorter focal length lens is used to give the same field of view as a camera with a larger sensor. That smaller lens has a smaller clear aperture and thus collects less light in the same exposure time, even if at the same f/ratio as a larger lens on a larger camera.
Consider a 20 mm f/2.8 lens. The clear aperture is only 20/2.8 = 7.14 mm in diameter. Now consider a 50 mm f/2.8 lens, which has a clear aperture of 50/2.8 = 17.86 mm. The 50 mm f/2.8 lens collects 6.25 times as much light as the 20 mm f/2.8 lens. Now consider the above lenses on a full frame (24x36 mm) DSLR and compare it to a point and shoot (P&S) camera with a sensor 5 times smaller and a lens with an equivalent field of view as the 50 mm lens. The P&S lens would have a real focal length of 50/5 = 10 mm to give the same field of view (this is what equivalent means: the field of view and not other parameters). That 10 mm lens at f/2.8 would only have a clear aperture of 10/2.8 = 3.57 mm. Thus, the 10 mm would collect a mere 25 times less light in the same exposure time! This huge difference in light gathering ability by the tiny lens is what has erroneously been attributed to small sensor and small pixel sensitivities. Again, it is not the sensor, but the lens that is key to gathering light because all digital camera sensors are reasonably close in efficiency compared to the huge differences in lens clear apertures.
Even with the same sensor, the same f/ratio, same ISO, and same exposure time, the lens with the larger clear aperture will gather more light on a subject. The images in Figure 5a and 5b demonstrate this basic rule: the larger clear aperture lens collects more light, recording more and fainter stars, even at the same f/ratio. Note that in Figure 5, the 50 mm lens also recorded more light from the sky background.

Figure 5a. Using the same sensor (Canon 1D Mark IV digital camera),
the same exposure time (30 seconds), same ISO (1600; remember ISO does
not change sensitivity), same f/ratio (f/2.8), the larger aperture lens
collects more light (the 50 mm lens, image on the left) than the
smaller aperture lens (20 mm focal length lens on the right). Both
images are crops of 1 original camera pixel to one image pixel
shown here. Both images have exactly the same processing. The image
made with the 50 mm lens not only shows more and fainter stars,
but recorded more light from the sky background.

Figure 5b. Natural color images. Comparison of best effort processing of two images, both made
with f/2.8 lenses, ISO 1600, 30 second exposures with the same sensor. The
35 mm f/2.8 lens collects 5.4 times the light from the SUBJECT as the 15
mm f/2.8 lens. The higher noise in the 15 mm image is due to the lower
light, combined with light levels so low that fixed pattern noise from
the sensor also contributes. Both images are crops from the full frame
and downsized for presentation. The proportion of noise on a subject is
the same in the original images. Sky conditions were slightly worse for
the 35 mm image with more haze which also added to the light pollution,
yet the larger lens produced a better image despite worse conditions. (The
bright stars are somewhat enlarged due to haze in the atmosphere.)
Daylight white balance.
The rule in photography is that for a given f/ratio lens, the light per unit area per time should be a constant. This means there should be little difference in the sky background between the 50 mm f/2.8 lens and the 20 mm f/2.8 lens. The reason is that the smaller aperture of the 20 mm lens collects less light, but collects light from a larger area of the sky for each pixel, cancelling the effects of the smaller aperture. Stars, are different because they are diffraction disks and further spread by lens aberrations and their size is not dependent on focal length.
The shorter focal length wider angle lenses tend to have more elements to correct all the aberrations and thus appear to have lower transmission than the simpler longer focal length lenses. Note the 50 mm lens I used was the Canon 50 mm f/1.8 version II lens which is around a decade old. The 20 mm lens was the Canon 20 mm f/2.8 lens and is about 4 years old. In any case, the longer focal length lens wins by clear aperture, and may possibly be boosted by better transmission.
An additional factor in image quality is detail. The longer focal length lenses gather more light, and provide more detail, but cover less angular area of the scene. Because the stars move relatively slowly, multi-image mosaics are feasible.
I have found a compromise solution to a large field of view and large clear aperture: the 24 mm f/1.4 lens. This lens suffers from significant aberrations wide open, but produces reasonable images at f/2, especially on cropped sensors like the 1D Mark IV (1.3x crop) or 7D (1.6x crop). A 24 mm f/2 lens has a clear aperture of 12 mm, thus collects a significant amount of light in a short exposure. Better is the 35 mm f/1.4 lens used at f/1.4 to make the image in Figure 1: very good stars to the corner of a full frame camera.
Clear aperture is key to recording stars (meteors too). Table 1 shows the effect of clear aperture for some lenses.
Table 1
============================================================================================================
A B C D E F G H I J
----Lens----- Clear Angular Coverage Angular Number of Stars Exposure Relative
Focal f/ Aperture Aperture of a 35 mm frame Area Factor: Time Meteor
Length ratio Diameter Area in degrees Covered Aperture Area Limited Efficiency
(mm) (mm) (square mm) Long Short (sq. degrees) * Angular Area Factor Factor
(sq mm * sq degrees) (col H / A)
10 4 2.50 4.91 121.89 100.39 12236.48 60066 1.20 6007
14 2.8 5.00 19.63 104.25 81.20 8465.37 166217 2.37 11873
15 4 3.75 11.04 100.39 77.32 7762.03 85729 1.14 5715
15 2.8 5.36 22.54 100.39 77.32 7762.03 174957 2.33 11664
16 2 8.00 50.27 96.73 73.74 7133.07 358547 4.48 22409
18 3.5 5.14 20.77 90.00 67.38 6064.21 125972 1.40 6998
18 2.8 6.43 32.46 90.00 67.38 6064.21 196831 2.19 10935
18 1.8 10.00 78.54 90.00 67.38 6064.21 476282 5.29 26460
20 2.8 7.14 40.07 83.97 61.93 5200.33 208384 2.08 10419
20 1.4 14.29 160.29 83.97 61.93 5200.33 833536 8.34 41677 **
24 2.8 8.57 57.70 73.74 53.13 3917.80 226068 1.88 9419
24 2 12.00 113.10 73.74 53.13 3917.80 443093 3.69 18462
24 1.4 17.14 230.81 73.74 53.13 3917.80 904272 7.54 ** 37678
28 3.5 8.00 50.27 65.47 46.40 3037.64 152689 1.09 5453
28 2.8 10.00 78.54 65.47 46.40 3037.64 238576 1.70 8521
28 1.8 15.56 190.05 65.47 46.40 3037.64 577295 4.12 20618
30 2 15.00 176.71 61.93 43.60 2700.21 477167 3.18 15906
35 2.8 12.50 122.72 54.43 37.85 2060.22 252827 1.44 7224
35 2 17.50 240.53 54.43 37.85 2060.22 495541 2.83 14158
35 1.4 25.00 490.87 54.43 37.85 2060.22 1011309 5.78 * 28895
50 2.8 17.86 250.45 39.60 26.99 1068.80 267677 1.07 5354
50 2 25.00 490.87 39.60 26.99 1068.80 524647 2.10 10493
50 1.8 27.78 606.02 39.60 26.99 1068.80 647712 2.59 12954
50 1.4 35.71 1001.78 39.60 26.99 1068.80 1070707 4.28 21414
50 1.2 41.67 1363.54 39.60 26.99 1068.80 1457352 5.83 29147
85 1.4 60.71 2895.15 23.91 16.07 384.32 1112662 2.62 13090
85 1.2 70.83 3940.63 23.91 16.07 384.32 1514456 ** 3.56 17817
100 2 50.00 1963.50 20.41 13.69 279.29 548392 1.10 5484
105 1.4 75.00 4417.86 19.46 13.04 253.69 1120757 2.13 10674
200 2.8 71.43 4007.13 10.29 6.87 70.63 283038 0.28 1415
300 2.8 107.14 9016.05 6.87 4.58 31.46 283649 0.19 945
lenses at f/2 compared:
24 2 12.00 113.10 73.74 53.13 3917.80 443093 3.69 * 18462
35 2 17.50 240.53 54.43 37.85 2060.22 495541 2.83 14158
50 2 25.00 490.87 39.60 26.99 1068.80 524647 2.10 10493
100 2 50.00 1963.50 20.41 13.69 279.29 548392 1.10 5484
============================================================================================================
Exposure Time Limited Factor = the Number of Stars factor * equation 1 exposure time /1,000,000
* Author's choice for an excellent nightscape lens.
** Maximum value in this column.
In the above table, the "Number of Stars Factor" is a relative number
indicating how the lens performs in terms of recording stars and meteors,
or other light sources. For each lens. If you work at a lower f/stop,
reduce the factor by 2 for each slower f/stop. Because most lenses are
not used wide open on nightscapes due to aberrations, above 1,000,000
are not achievable, except in some rare cases. For example, a 24 mm
lens at f/2 has a factor of 564164, a very high number. The 35 mm lens
at f/2 is higher at 630943 and the 50 mm at f/2 is 668001. All three
of these lenses will provide excellent results, but exposure times will
limit the longer focal length due to star trailing (if one wants to keep
stars untrailed) when using a fixed tripod. The last column, "Exposure
Time Limited Factor" takes into account the limits of exposure time as a
function of focal length from equation 1, below. if we only look at f/2
lenses, the 24 mm f/1.4 lens at f/2 comes out on top with this factor.
It is a nice compromise in sky coverage and light collecting ability.
If you are using a cropped sensor camera, the factors in the last two
columns drop with the square of the crop, but the lenses with better
light gathering ability still retain there same relative positions.
The bottom line is the last column, Exposure Time Limited Factor,
applies best for fixed tripod mounted cameras where the exposure time
must be kept short enough to keep stars round. The second to last column,
Number of Stars Factor, is best when tracking the stars.
Table 2 shows the faintest star that can be recorded in a 30-second exposure with a modern digital camera. Larger stellar magnitudes are fainter stars. Five stellar magnitudes equals a factor of 100 in brightness so a magnitude 10 star is 100 times fainter than a magnitude 5 star. The faintest star visible with the unaided human eye is typically about 7 to 7.5 in very dark skies away from city lights (Clark, 1990). Table 2 indicates the telescope required for a visual detection of stars as faint as can be recorded with the given lens and a digital camera and a 30-second exposure
There is an additional factor not seen in Table 1. As the camera records fainter stars, more stars appear in greater numbers than the light gathering. For example, double the collections area or double the exposure time, more than twice as many stars will show. That biases the number of stars factor in favor of the larger aperture lenses. An example of this effect is shown in Figure 5b.
Table 2
Faintest star recorded in a 30-second exposure, dark skies, modern digital camera
=========================================================================================================
Aperture Aperture Exposure CEF Telescope aperture needed to visually
Lens Diameter Area Time (sq. cm * Stellar see these stars
FL (mm) f/ratio (mm) (sq. cm) (minutes) minutes) Magnitude (inches) (cm)
10 2.8 3.6 0.10 0.5 0.050 8.7
14 2.8 5.0 0.20 0.5 0.098 9.5
15 4 3.8 0.11 0.5 0.055 8.8
15 2.8 5.4 0.23 0.5 0.113 9.6
16 2 8.0 0.50 0.5 0.251 10.5
17 2.8 6.1 0.29 0.5 0.145 9.9
20 2.8 7.1 0.40 0.5 0.200 10.2
24 2.8 8.6 0.58 0.5 0.289 10.6
24 2 12.0 1.13 0.5 0.565 11.4
24 1.4 17.1 2.31 0.5 1.154 12.1 2 5 (e.g. 7x50 binoculars)
28 3.5 8.0 0.50 0.5 0.251 10.5
28 2.8 10.0 0.79 0.5 0.393 11.0
28 1.8 15.6 1.90 0.5 0.950 11.9
28 1.4 20.0 3.14 0.5 1.571 12.5
35 2.8 12.5 1.23 0.5 0.614 11.4
35 2 17.5 2.41 0.5 1.203 12.2
35 1.4 25.0 4.91 0.5 2.454 13.0 3 7.5 (e.g. 10x80 binoculars)
50 2.8 17.9 2.50 0.5 1.252 12.2
50 2 25.0 4.91 0.5 2.454 13.0
50 1.8 27.8 6.06 0.5 3.030 13.2
50 1.4 35.7 10.02 0.5 5.009 13.7 4 10
50 1.2 41.7 13.64 0.5 6.818 14.1
85 1.2 70.8 39.41 0.5 19.703 15.2
85 1.4 60.7 28.95 0.5 14.476 14.9
85 2 42.5 14.19 0.5 7.093 14.1
100 2 50.0 19.63 0.5 9.817 14.5 6 15
105 1.4 75.0 44.18 0.5 22.089 15.3
200 2.8 71.4 40.07 0.5 20.036 15.2 8 20
300 2.8 107.1 90.16 0.5 45.080 16.1 12 30
400 2.8 142.9 160.29 0.5 80.143 16.7
500 4 125.0 122.72 0.5 61.359 16.4
600 4 150.0 176.71 0.5 88.357 16.8 18 46
=========================================================================================================
For other exposure times, the increase in signal from an object increases linearly with exposure time, but so does the background sky. The combined light is star + sky, so to push to fainter stars with more exposure time means the faintest star one can record (magnitude value) increases as the square root of the exposure time.
The stellar magnitude difference = -2.5*log10(brightness ratio), and conversely,
brightness ratio = 10(-0.4 * stellar magnitude difference)
The
Clark Exposure Factor, CEF,
is:
CEF = (pi/4) * (aperture diameter in cm)2 * time in minutes, pi = 3.14159.
Putting aperture and exposure time together, signal increases with aperture area and exposure time.
Signal-to-Noise ratio (S/N, or SNR) on stars increases as the aperture area and the square root of the exposure time, assuming the exposure is sky brightness limited. If the camera is read noise limited, then faintest star increases with aperture time exposure time (CEF) instead of the square root of the exposure time. Most night photography, and the values in Table 2 use the sky brightness limited case. The S/N on extended objects increases with the square root of the CEF. At high magnifications, stars are blurred by atmospheric turbulence (called seeing), so then stars are also treated as extended objects and faintest star increases with the square root of the CEF. Using the common case of sky brightness limited, low magnifications as typically found in nightscape photography leads to the equation:
faintest star = K + 2.5 * log10( aperture area * square root( exposure time)),
where K is a constant that depends on camera sensitivity (that is NOT ISO; it is quantum efficiency times optics transmission), atmospheric conditions and units. In Table 2, K = 11.6 with time in minutes, and aperture area in square centimeters, for the green channel of a Bayer sensor digital camera. The value used is for moderate altitudes (about 20 to 30) degrees up from the horizon for clear mountain air at about 7000 feet elevation (2000 meters), and low humidity. Note sensor size is not part of the equations because sensor size does not impact system sensitivity.
For other conditions, adjust the value of K up and down. For example, at 9600 feet from a very dark site, clear air, low humidity, my Canon 6D Mark II + 105 mm f/1.4 camera records stars 0.7 magnitude fainter than the above table when pointing straight overhead, so K = 12.3. For a city with a couple of million people, a red zone on the light pollution map, 45 degrees up from the horizon, K ~ 8.7, or about 4 magnitudes worse than at a dark site away from cities.
Below is a summary. For more details, see Part 4d) Meteor Photography
In Table 1 I listed the relative meteor efficiency factors for various lenses, while Table 2 lists faintest stars for various apertures and a 3o second exposure. But meteors travel fast, and the longer the focal length, the faster the meteor will move across a pixel. Combining Tables 1 and 2, and assuming an average pixel gets exposed by a meteor 1/100 second with a 35 mm focal length, Table 3 lists meteor efficiency and faintest meteor magnitudes one might expect. Of course there are many variables, including actual meteor speed, light pollution, and pixel size, so consider this a relative scale. All the values scale with sensor size as a smaller sensor covers less angular area, which lowers the probability of catching a meteor.
For Canon users, my top choice for a meteor camera (and a nightscape camera) is Canon 6D 20-megapixel digital camera, with a Sigma 35 mm f/1.4 DG HSM lens used at f/1.4 and ISO 1600. Then I would frame continuously with 30 second exposures from a dark site (shorter if the sky is brighter) on a stable tripod. You could also have the camera on a tracking mount so the stars stay round.
Table 3
============================================================================================================
A B C J
----Lens----- Clear Relative Faintest star Faintest Meteor Best Meteor Lens
Focal f/ Aperture Meteor Stellar Magnitude Relative
Length ratio Diameter Efficiency (30-second Exposure Stellar Magnitude Meteor Efficiency
(mm) (mm) Factor exposure) (seconds) larger number = * Meteor Stellar
(from Table 1) better (fainter) Magnitude /10000
10 4 2.50 6007 8.7 0.035 0.4 0.2
14 2.8 5.00 11873 9.4 0.025 1.5 1.8
15 4 3.75 5715 8.8 0.023 0.8 0.5
15 2.8 5.36 11664 9.5 0.023 1.6 1.9
16 2 8.00 22409 10.4 0.022 2.4 5.4
18 3.5 5.14 6998 9.5 0.019 1.3 0.9
18 2.8 6.43 10935 9.9 0.019 1.8 2.0
18 1.8 10.00 26460 10.9 0.019 2.8 7.3
20 2.8 7.14 10419 10.2 0.018 1.9 2.0
20 1.4 14.29 41677 11.7 0.018 3.4 14.3 **
24 2.8 8.57 9419 10.6 0.015 2.1 2.0
24 2 12.00 18462 11.3 0.015 2.8 5.3
24 1.4 17.14 37678 ** 12.1 0.015 3.6 13.6 *
28 3.5 8.00 5453 10.4 0.013 1.8 1.0
28 2.8 10.00 8521 10.9 0.013 2.3 1.9
28 1.8 15.56 20618 11.9 0.013 3.2 6.7
35 2.8 12.50 7224 11.4 0.010 2.5 1.8
35 2 17.50 14158 12.1 0.010 3.3 4.6
35 1.4 25.00 28895 + 12.9 0.010 4.0 11.6 +
50 2.8 17.86 5354 12.2 0.007 2.9 1.6
50 2 25.00 10493 12.9 0.007 3.6 3.8
50 1.8 27.78 12954 13.1 0.007 3.9 5.0
50 1.4 35.71 21414 13.7 0.007 4.4 9.5
50 1.2 41.67 29147 * 14.0 0.007 4.8 13.8 *
85 1.2 70.83 17817 15.2 0.0041 5.3 9.5
100 2 50.00 5484 14.4 0.0035 4.4 2.4
lenses at f/2 compared:
24 2 12.00 18462 11.3 0.015 2.8 5.3
35 2 17.50 14158 12.1 0.010 3.3 4.6
50 2 25.00 10493 12.9 0.007 3.6 3.8
100 2 50.00 5484 14.4 0.0035 4.4 2.4
============================================================================================================
** Maximum value in this column.
* Second in this column
+ Third in this column
Example using the a full-frame 35 mm digital camera and 35 mm f/1.4 lens: gives an angle of view of 54.4 x 37.9 degrees, or about 2062 square degrees. There are about 20626 square degrees in the visible sky, so the 35 mm focal length lens covers about 10% of the sky. If the meteor rate were 60 meteors per hour observable visually, we could expect about 6 meteors per hour to be recorded by a 35 mm lens on a full frame camera if the sensitivity were similar to our eyes. But a 35 mm f/1.4 lens has an aperture of 25 mm, compared to dark adapted eyes of about 7 mm. That means the 35 mm f/1.4 lens collects (25/7)2 = 12.7 times more light. Digital camera sensors are several times more sensitive than our eyes (let's say 5x), thus the digital camera would record about:
meteor record rate ~ visual rate * lens sky coverage fraction * (lens/eye area ratio) * sensitivity increase
For 60 meteors per hour and a 35 mm f/1.4 lens on a full frame camera:
meteor record rate ~ 60 * 0.1 * 12.7 * 5 = 381 / hour, about 3 per 30-second exposure!
For a 15 mm f/2.8 lens on a 1.6x crop body (73.2 x 52.8 degrees) ~ 19% of the sky,
and an area ratio of 0.58, the camera + lens would record:
meteor record rate ~ 60 * .19 * .58 * 5 ~ 33 per hour ~ 1 per two-minute exposure.
The main issue in making nightscape images is focusing in such low light conditions. I have found that focusing wide angle lenses with autofocus misses accurate focus most of the time using stars. Autofocusing with telephoto lenses usually works well in my experience. To focus wide angle lenses, I use live view, increase magnification on the LCD screen to 10x, and use a 5x magnifier to examine the image of bright stars. I then focus manually. Be aware of any blur both inside and outside of best focus. On some lenses, the inside focus blur will be one color (e.g. red) while outside focus blur will be a different color (e.g. blue). If there is any hint of red halos, the images will generally be less pleasing, so if anything, bias to having a blue halo. For example, compare the images in Figure 4a, 4b which have a faint blue halo with whose from the 50 mm lens in Figure 5, which has a reddish-magenta halo. I used autofocus on the 50 mm image and the focus was slightly off from optimum.
As previously discussed, choose an ISO that boosts sensor read noise above camera electronics noise, especially banding noise. If you are unsure of the correct ISO, try some night sky images at ISO 800, 1600, and 3200. Examine each for banding noise, and choose the lowest ISO with the least banding noise in the background sky.
The main reason for high ISO in my opinion is to get framing correct before the real image is taken. I use high iso (1600 to 6400) for focusing on a star with live view, then quick exposures for framing. Then drop back to ISO 1600 (3200 on the 5D Mark II) for the real exposures for better dynamic range.
For natural color, use daylight white balance.
If you want to keep star images reasonably round, exposure times must be short enough to prevent trailing. When imaging near the celestial poles, exposure times can be longer, but if near the celestial equator (e.g. the constellation Orion), exposure times must be much shorter.
Digital cameras typically have significantly finer resolution than film, so the old rules of exposure times to prevent star trailing no longer apply. For a 24 mm lens, exposure times near the celestial equator should about 8 seconds maximum. This leads to the equation:
maximum exposure time in seconds = 200 / focal length in mm. (equation 1)
Exposure times for several lenses with this formula are shown in Table 4. Note that Table 4 shows that even though exposure times get shorter with with longer focal lengths, the aperture areas grown faster such that fainter stars are recorded.
Table 4
Faintest star recorded on a Fixed Tripod with
Exposure Limited to Keep Stars Round (200 Rule)
modern digital camera
============================================================
Maximum
Aperture Aperture Exposure Faintest Star
Lens Diameter Area Time (Stellar
FL (mm) f/ratio (mm) (sq. cm) (seconds) Magnitude)
10 2.8 3.57 0.10 20.0 8.5
15 2.8 5.36 0.23 13.3 9.2
17 2.8 6.07 0.29 11.8 9.4
20 2.8 7.14 0.40 10.0 9.6
24 1.4 17.14 2.31 8.3 11.4
28 1.4 20.00 3.14 7.1 11.7
35 1.4 25.00 4.91 5.7 12.1
35 2.8 12.50 1.23 5.7 10.5
50 1.2 41.67 13.64 4.0 13.0
50 1.4 35.71 10.02 4.0 12.6
50 1.8 27.78 6.06 4.0 12.1
100 2 50.00 19.63 2.0 13.0
200 2.8 71.43 40.07 1.0 13.4
300 2.8 107.14 90.16 0.7 14.0
300 2.8 107.14 90.16 0.7 14.0
400 2.8 142.86 160.29 0.5 14.5
500 4 125.00 122.72 0.4 14.1
600 4 150.00 176.71 0.3 14.4
============================================================
If the above exposure times are insufficient, make multiple exposures with the above guidelines and average them together with your photo editor. For example, stack them in layers in photoshop and set the layer opacity to the inverse of the number of layers. For example, with 3 images, 8-seconds each, set layer opacity to 33% on all but the bottom layer. If your photo editor can average the images, that will also work.
On the internet, one sees other formulae for keeping stars pinpoints. A popular one is the 500 rule:
for slightly trailed stars: maximum exposure time in seconds = 500 / focal length in mm. (equation 2)
A demo with technical details why the 500 rule produces trailed star images is shown in Figure 6a, 6b. The star field is for 30 degrees from the celestial equator. If on the celestial equator, the trails would be 15% longer. The 500 rule for a 35 mm lens would be 500/35 = 14.2 seconds. The image clearly shows star trailing at 14 seconds. The computed trail is 4.7 pixels. At 11 seconds, the trailing is 3.7 pixels and the formula would be 385/focal length in mm, but that too is clearly too long.
At 8 seconds, the drift would be 2.7 pixels and would produce oval stars (Figure 6a), but would be slightly worse on the celestial equator. Six seconds would produce pretty good stars (Figure 6b). At 6 seconds, the rule would equate to 210/focal length in mm, close to equation 1. For cameras with smaller pixels, shorter exposure times are needed in order to keep stars round.

The more technical equations for keeping stars round. Stars on the celestial equator move 15 arc-seconds per time second. So compute the angular size of a pixel to determine the star drift rate. The pixel pitch is called the Plate Scale:
plate scale = 206265 * pixel size in mm / focal length in mm.
The 206265 factor is the number of arc-seconds in one radian. There are 1000 microns in one mm. Determine pixel pitch by:
Sensor long edge in MM / long edge in pixels = pixel pitch
For example, The Canon t5i has a 22.3 x 14.9 mm sensor and image size 5,184 x 3,456 pixels, so the pixel pitch is 22.3 / 5184 = 0.0043 mm.
For a Canon T5i or 7D with 4.3 micron pixels (0.0043 mm), the plate scale with an 18 mm focal length lens is:
plate scale = 206265 * 0.0043 / 18 = 49.3 arc-seconds.
A star will cross one pixel every 49.3 / 15 = 3.29 seconds.
For stars not on the celestial equator, simply divide the exposure time by the cosine of the Declination to get the same drift amount in pixels. Or multiply by the cosine of the Declination to get the drift amount in pixels for the same exposure time. For example, at Declination 45 degrees, cosine(45) = 0.7071, so the example above with 3.29 seconds for 1 pixel drift could be increased to 3.29 / 0.7071 = 4.65 seconds. At 3.29 seconds, the drift would be 1 pixel * 0.7071 = 0.7071 pixel.
The 500 rule above (500/18 = 28 seconds) would give star trailing of 28 / 3.29 = 8.5 pixels or the 500 rule divided by crop factor (500/1.6= 312 rule) would give 300/17 = 17 seconds. With a 17 second exposure one would get 17 / 3.29 = 5.2 pixels with a T5i camera and 18 mm focal length lens.
More information on Image Plate Scale can be found here.
A couple of pixel trail will be noticeable with a sharp lens. So a 200 rule is needed for actual round images with good lenses. If you are imaging near the celestial poles, exposure times can be longer. Half way between the celestial equator and the pole, exposure times can be 40% longer and not show trailing (technically, divide the exposure time by the cosine of the Declination of the star to get the maximum exposure time for stars away from the celestial equator).
The exposure times above for a static camera are really too short to collect enough light to record many stars. To keep star images round with long exposure times, one must track the stars to compensate for the rotation of the Earth. In a nightscape, that tracking stars means any terrestrial landscape objects would get blurred. My solution on such frames is to make two exposures: one with tracking on for stars, and one with no tracking for the static scene. Then I stack to two images in a photo editor and select the sky from the tracked image and the landscape from the untracked image and merge the two. In making such exposures, the tracked and untracked pair should be done one right after the other. An example is shown in Figure 7.

Tracking can be done with sophisticated telescope mounts,
like German Equatorial or fork mounts, or with simple
"barn Door tracking mount"
http://clarkvision.com/articles/barn.door.tracking.mount/.
Such a simple tracking mount weights less than a kilogram (2.2 pounds)
including the ball head. Figure 7 was made with this simple barn door
tracking mount.
Star trails are simpler in that long exposures can be used. When using long exposures, the lens aperture can be reduced (slower f/ratio) to prevent overexposure. A cable release is needed if exposure times are longer than the camera maximum (usually 30 seconds). You can also make multiple exposures, e.g. 30 seconds to a few minutes, and combine them into one image. Combine using maximum signal rather than average. For example, put each image in a layer, and set layer type to lighten.

Being out in dark places can be a safety hazard, from working in the dark and tripping over something, to predator animals, to dangerous people. If in bear country, I carry bear spray. Be sure and take appropriate precautions.
I will no longer go out alone at night in this environment, even at a lodge. Arrange for a local guard to meet you at your room and stay with you while doing such images (and tip them well).

When doing long exposures, if one is concerned about shadow detail and color, one should make dark frames and subtract them. Performance could be substantially better in a hotter night when dark current noise is higher. For temperatures lower than typical room temperatures and exposures of 30 seconds or less, dark frame subtraction with modern cameras is usually not needed. One can even take darks on a different night, as long as they are near the same temperature. The images in Figure 1, 7, and 8 did not have any dark frames subtracted. Digital cameras older than about circa 2008 had issues with dark levels and required dark frame subtraction.
To maximize signal-to-noise ratios, record raw. Depending on the raw converter settings, stars may get colored halos with some settings. For example, some of the stars in Figure 1 show magenta stars. The magenta stars are an artifact of photoshop Adobe Camera Raw (ACR) raw conversion and are not all true colors, except for some red and orange stars. The problem occurs with the camera profile set to Adobe Standard. This causes saturated stars to have a black ring (image values =0) in the green channel, leaving blue and red, which makes magenta. The solution is to set the camera profile to Camera Faithful. A slight mis-focus on lenses with chromatic aberration can also cause magenta star colors, which can be further enhanced with raw processing.
In raw conversion, set black point to zero. Never add exposure or brightness to the image as it will wash out star colors. In fact, in the raw converter, pull exposure 1 stop! This is contrary to the idea of push the signal higher, but pulling one stop will keep better star colors. Boost in post processing with curves to bring up the faint portions of the image and not blow out star colors.
In post processing, never use the shadow/highlight tool on such images as it is additive and produces strange artifacts. I only adjust image intensity with curves, which is a multiplicative tool. If one needs to subtract (e.g. light pollution), then the left slider on the levels tool does that. I'll never use the right slider on the levels tool as that will cut off star intensity, destroying color.
Star clouds can be enhanced with unsharp mask, radius 30 to 40, amount around 30 to 50, and low thresholds like 3 to 10. This also enhances stars.
Nightscape imaging can be successful using a variety of equipment. Camera sensor size and pixel size is largely irrelevant. The success in nightscape imaging is to use the largest clear aperture diameter lens you can obtain. ISO does not change sensitivity, but is used to boost faint signals from the sensor above camera electronics noise.
References and Further Reading
Clark, R.N. (1990), Visual Astronomy of the Deep Sky, Cambridge University Press and Sky Publishing, (book of 355 pages).
Clarkvision.com Nightscapes Gallery.
1) Night and Low Light Photography with Digital Cameras
http://clarkvision.com/articles/night.and.low.light.photography/
2) Digital Camera Sensor Performance Summary
http://clarkvision.com/articles/digital.sensor.performance.summary
3) The f/ratio Myth and Digital Cameras
http://clarkvision.com/articles/f-ratio_myth
4) Digital Cameras: Does Pixel Size Matter?
http://clarkvision.com/articles/does.pixel.size.matter
5) Digital Cameras: Does Pixel Size Matter?
Part 2: Example Images using Different Pixel Sizes
http://clarkvision.com/articles/does.pixel.size.matter2
The Night Photography Series:
| Home | Galleries | Articles | Reviews | Best Gear | Science | New | About | Contact |
http://clarkvision.com/articles/nightscapes
First Published October 20, 2012
Last updated August 20, 2018