Best Camera Characteristics for Low Light Photography
Summary Regarding Selecting a camera
Details
Contrary to popular internet opinion, the main factor, after lens aperture
in long exposure photography, e.g. about a minute and longer, or even
tens of seconds in warm environments, is noise from dark current. Popular
internet opinion focuses on read noise, but read noise is insignificant
in long exposures compared to noise from light pollution, airglow, and dark current,
especially when used with lenses faster than about f/4. One can only beat
light pollution in full color imaging by imaging the night sky far
from cities, but dark current goes with the camera. Dark current is very
camera dependent, and few reviews measure it. Dark current is measured
in many reviews here on Clarkvision.
Low dark current is a key factor in long exposure low light photography.
First some facts about dark current. Dark current doubles every few
degrees increase in temperature. Typically, the doubling in CMOS sensors
is every 5 to 6 degrees Centigrade. To be really precise with dark
current subtraction (used in astrophotography), one needs the dark
current to be measured at the same temperature to within a fraction of
a degree. Noise from dark current is the square root of the dark current
from the total exposure time (including stacking) and is independent
of sub-exposure times. For example, if you make 50 1-minute exposures
using a camera with 1 electron/second dark current, the noise from dark
current in the stacked image is square root ( 50 exposures * 60 seconds per minute *1 minute) = 55 electrons.
Another big factor in image quality in nightscape and astrophoto images
is banding in the camera. Banding is a fixed pattern usually horizontal and/or vertical.
We are very sensitive to detecting banding so it becomes objectionable
even when the peak-to-peak banding is 10 times smaller than random noise in the
image. Some cameras have banding problems at some ISOs and not others.
As ISO is increased, banding problems usually decrease.
Banding is shown in reviews here on Clarkvision.
There is one camera that I have tested or seen data from other testing
that stands well above the others: that is the
Canon
7D Mark II digital camera
(Figure 6, below). See the
7D Mark II review here and look at Figure 3 and Table 3 of the
review and the corresponding discussion. Some recent Sony and Nikon
numbers by people on dpreview indicate dark currents similar or slightly
better than the other Canon cameras on Figure 6 below but I have not seen
any data better than that for the 7D2.
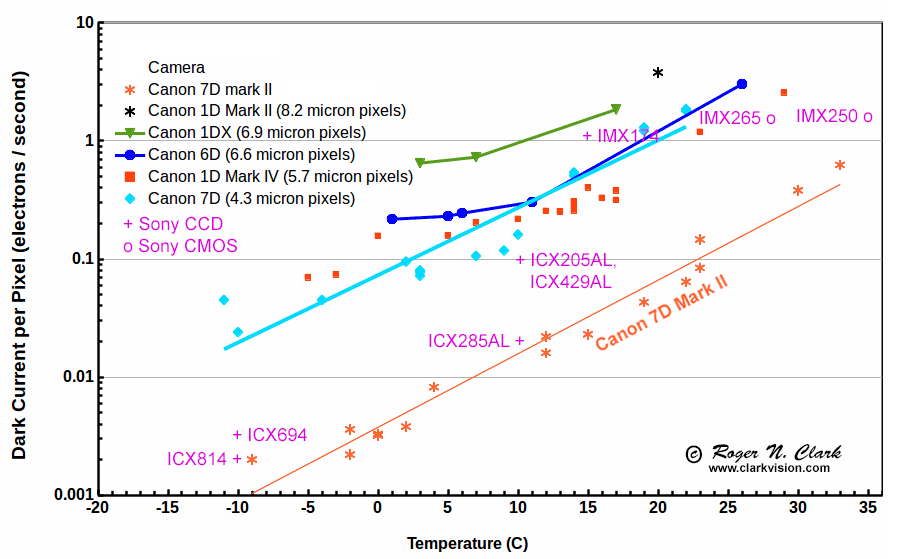
Figure 6. Dark current for several cameras is compared as a function of internal
camera temperature. Note the amazing improvement in low dark current with the
Canon
7D Mark II digital camera.
Sony sensor data are from commercial data sheets found online.
Newer model cameras from all manufacturers generally have better sensors,
with lower noise (banding, read noise, dark current), so choose the latest
model cameras for best results, especially if they have reviews that
show if the camera has banding issues and a measurement of dark current.
Key new technology is called dark current suppression.
Dark current suppression technology is hardware and part of the pixel design.
It is not something your turn on or off in software. It is not
long exposure noise reduction. It is not high ISO noise reduction.
The hardware in the latest sensors use a 4-transistor circuit in
the pixel. Some use 3 transistors. This is called 4T and 3T designs.
What dark current suppression technology does is block the signal, but
not the noise from dark current. The technology became established in
circa 2008 digital camera models, and has been refined with newer models.
What this means is in sensors that have the technology, we do not need to
measure dark frames and subtract them in post processing. We no longer
see amp glow in long exposure images (usually seen as pink blobs on the
edges of frames). This technology allows a big simplification in post
processing. If your camera shows
amp glow, it would be a benefit to upgrade to a newer camera (models
post circa 2008). The newest models generally have better refinements,
meaning longer and longer exposures without the problems so common in older models.
Figure 7 shows the major advance in technology that dark suppression and other sensor
improvements have enabled in the last decade. If you have an older camera,
pre 2010 and certainly pre 2008, an upgrade to a very recent model
can be a big benefit.
See
Part 7b) On-Sensor Dark Current Suppression Technology
of this series for more detail.

Figure 7. Comparison of technology. The image on the left was obtained
in 2005 and on the right 2015. The image on the right collected 36% more light
per pixel, so if technology were equal, the apparent noise difference would be
only about 17%, barely noticeable. Obviously, the improved sensitivity
and lower noise of modern cameras makes a huge difference.
See the
gallery image of the 2015 image here. The 2015 image was made with a Canon
7D Mark II 20-megapixel digital camera and 300 mm f/2.8 L IS II lens plus a
Canon Extender EF 1.4X III
giving 420 mm at f/4 and ISO 1600.
Another thing to consider in selecting cameras with low dark current
(remember, the dark current suppression technology blocks the dark current
level, but not the noise), is camera models that will dissipate heat
more efficiently. The large massive pro cameras are at a disadvantage
here. Their shear mass, generally faster electronics, more electronics
(e.g. dual cpus), mean more heat and the heat that gets generated is
harder to dissipate with all that mass. Lighter smaller cameras tend
to dissipate heat better, and with slower electronics, generate less heat.
But regardless of new camera, you will see the biggest impact on image quality by getting
quality lenses with larger apertures. For example, 24 mm f/1.4, 35 mm
f/1.4, 50 mm f/1.4. The Sigma Art series are excellent. Rokinon/Samyang
are cheaper but be aware people are finding they need to return multiple
lenses before getting a good copy.
Crop versus Full Frame Cameras
Contrary to popular internet belief, larger sensor cameras have little to do
with sensitivity. We often read on the internet that full frame cameras
are more sensitive and that they are better at low light photography.
This is a misunderstanding of the light gathering of lens and sensor.
A larger format ENABLES one to use a larger lens. It is
the lens that collects the light; the sensor is just a bucket to collect
the light delivered by the lens (Figure 8).
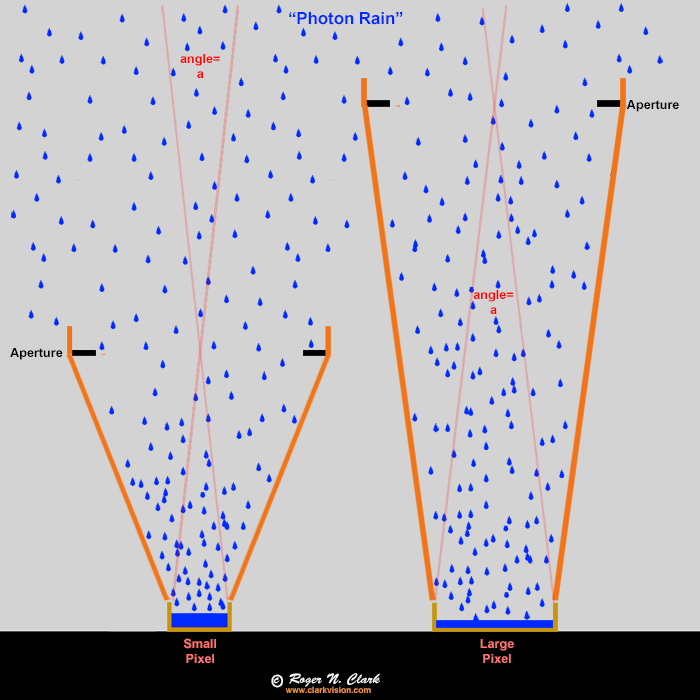
Figure 8. Raindrops (blue) as an analogy to photons entering a
camera. The buckets ("pixels") fill with water (blue), but the orange
funnels (the lens) collect the rain and focus it onto the buckets (pixels). In this
case the large end of the funnels have the same diameter so collect the
same amount of rain per unit time (the exposure). The ONLY difference
is the small bucket will fill up faster, but that is not a problem in
low light situations. Small buckets are NOT a disadvantage. The funnel
diameter controls how much rain goes into the bucket, not the size of
the bucket. It is the same with cameras, lenses, and pixels. The angle
"a" is the is the angular size of a pixel and is the same for both the
large and small pixel in this example. In a camera, both cameras would
get the same amount of light per pixel, show the same noise, have the
same pixels on the subject, and have the same depth of field.
Example.
For a given field of view, e.g. a 35 mm on a full frame sensor gives a
54.4 by 37.8 degree field of view. To get that same field of view on a
1.6x crop camera, one needs a (35 / 1.6 =) 21.87 mm focal length lens.
Say the 35 mm lens was f/2.8, with an aperture diameter (35 / 2.8 ) =
12.5 mm. To collect the same amount of light with the 21.87 mm lens on
the crop camera, it would need the same aperture diameter (technically
called the entrance pupil) of 12.5 mm, making an f-ratio of 21.87 /
12.5 = 1.75. Typically, photographers keep the f-ratio constant,
thus compare a 35 mm f/2.8 on the full frame to 21.87 mm f/2.8 on
the crop. But a 21.87 mm f/2.8 lens has a smaller diameter aperture
(21.87 / 2.8 =) 7.8 mm, and collects 2.5 times less light from the
subject (12.5/7.8 squared)! The f-ratio tells light density, NOT total
light from the subject. This concept seems particularly confusing to
photographers trained that f/ratio tells about light. Yes, f-ratio
tells light density thus exposure, but not total light from the subject.
If you don't believe this, see Figures 9a, 9b and the text below, or if
you want to learn more see
part 1a of this series with Figures 4a, 4b, 5a, 5b and
my series on
Understanding Exposure.
Here is another way to look at the problem. Think of it this
way: you have a full frame camera and after you take the image, you crop
the image. You changed the field of view. You did not change the actual
focal length. A crop sensor is just a smaller sensor--think of it as
full frame pre-cropped so you don't have to crop in post processing. It
does not change the lens attached in any way--the focal length is the
same. The aperture is the same. The amount of light gathered within the
frame is the same. The smaller sensor just means a smaller field of view.
Why people think that changes sensitivity is surprising.
To understand effect of sensor size, try this analogy, we both go to
a hardware store, You buy a 5-gallon bucket, I buy a 1-gallon bucket.
We then go to a water faucet that is dribbling a low rate of water and
fill our buckets for 30 seconds. How much water do we each have in
our buckets? The amount of water in our buckets is not dependent on
the bucket size unless one bucket overflows, and with the low rate of
water from the faucet, neither bucket overfills (analogy to low light
photography). The amount of water in the bucket is dependent entirely
on the faucet delivering the water (analogy to the camera lens) and the
length of time of the fill (the exposure time). The amount of water
in the bucket has nothing to do with bucket capacity. We have the same
amounts of water in our buckets. It is the same with pixels: the amount
of light captured in the pixel is dependent on the lens delivering the
light. There is one additional factor in cameras and lenses: the area
the pixel covers. If we equalize the area, and thus pixels on subject,
then using the same lens, same f/ratio, same exposure time, the light
per pixel is the same, as in Figure 9a.
The lens delivers the light. The pixel is just a bucket. Below in
Figures 9a, and 9b are comparisons of images made with a full frame
and 1.6x crop cameras. If we believed the internet myth that larger
sensors are more sensitive, one would expect to see fainter stars in
the image made with the larger sensor and a noise difference between
full frame and crop cameras to be the square root of the pixel areas,
or sqrt(2.59) = 1.6, which would make the crop camera image noticeably
noisier. Clearly, that is not the case in Figure 9a. Web sites that
show a differences between crop and full frame cameras are typically
changing the lens aperture area between cameras, thus the amount of
light collected. If we keep the camera with small pixels at its full
resolution and enlarge the image from the camera with the larger pixels,
as in Figure 9b, we do see that the small pixels are noisier per pixel,
but there are more pixels in the same area as a pixel from the larger
pixel camera, thus the camera with smaller pixels show finer noise, and
more detail. And because the pixels are smaller, the stars are smaller,
and there is less contribution of noise from sky glow and dark current,
so the camera with smaller pixels shows substantially fainter stars.

Figure 9a. Comparison of images made with a full frame and 1.6x crop
cameras. The ratio of the pixel areas is 2.59. Focusing on the subject,
not the pixel (after all what is the subject in a photo: the subject,
or the pixel?), I binned the smaller pixels of the 1.6x crop camera
to the same pixels on subject in the full frame. By resampling to the
same pixel on the subject, we see that the signal-to-noise ratio (S/N)
is essentially the same in the uniform areas (agreement to better than
1 percent), but the smaller pixels of the crop camera actually record
fainter stars and more detail, even after resampling.
Compare the unbinned images in Figure 9b.

Figure 9b. Comparison of images from two cameras--the same as in Figure
9a, but the crop sensor image is shown at full resolution, and the full
frame camera enlarged 1.6x for comparison. The smaller pixels on the crop
camera record fainter stars, over 70% fainter (0.6 magnitude). The noise per pixel is
higher in the crop sensor camera, but there are more pixels, so the noise
appears smaller. There is also more fine detail in the crop sensor camera
image, thus providing better overall image quality despite technically
having more noise per pixel. And as shown in Figure 9a, when the pixel
angular areas are normalized, the noise is basically the same.
You can make great nightscapes and great astrophotos with both cropped sensors
and full frame sensors. I have made nightscape and astrophoto images with both cropped and
full frame cameras. My preferred astrophotography camera when I am doing
many minutes of exposure is a camera with low dark current, regardless of
sensor size. I pay less attention to sensor size in choosing a camera for a
low light job, and pay more attention to sensor characteristics like low dark
current and the lens that I will use.
The only other factor to consider regarding cameras is being able to change lenses.
Very fast wide angle lenses are only available in single focal lengths (commonly
known as prime lenses) with only a few
rare exceptions. Most zoom lenses are not as fast and produce lower
quality star images (again there are some exceptions).
This generally means a DSLR or mirrorless camera with interchangeable lenses.
Note that too much use of live view, whether mirrorless camera or DSLR
heats the sensor increasing dark current noise. Thus I prefer DSLRs
because I can frame and use the optical viewfinder to minimize sensor
heating. Once a sensor heats up, it can take a half hour or more
to cool back to ambient temperatures.
Long Exposure Astrophotography Considerations
Astrophotography with uncooled digital cameras has specific challenges.
As discussed above, dark current can be significant, and when imaging
in a low light pollution dark environment, dark current is usually the
limiting factor in imaging faint objects. Second, the light from galaxies,
nebulae and others interesting objects in the deep sky is very faint.
That means the largest aperture are you can put to work is important.
Dark current scales with pixel size, meaning larger pixels have more
dark current than smaller pixels.
This leads to the non-intuitive
concept of using the largest aperture to concentrate the light onto the
smallest pixels with telephoto lenses and amateur telescopes!

Figure 10a. The North America Nebula (NGC 7000) and the Pelican Nebula
(IC 5067, 5070) in natural color made with a stock
Canon EOS 90D DSLR Camera
and a
Canon 300 mm f/2.8 L IS II lens
the Canon 90D has 3.2
micron pixels. Total exposure time was 29.5 minutes.
Gallery image with more details.

Figure 10b. The Whirlpool Galaxy, M51.
This image was obtained with a Canon
7D Mark II 20-megapixel digital camera, a camera with small pixels and 300 mm f/2.8 L IS II lens plus a
Canon Extender EF 1.4X III
giving 420 mm at f/4, ISO 3200 and 2-arc-seconds per pixel.
Gallery image and more information is here.
Image scale is 2 arc-seconds per pixel.
Pixel Size. As I have already discussed, sensor size has little
to do with collecting light from the subject. Similarly, pixel size
also has little to do with light collection. The quantum efficiency (QE)
per square mm is the same (for the same technology) whether a tiny
sensor in a cell phone camera, or a full frame DSLR. This means if
you concentrate the same amount of light onto a spot 10 microns square
versus 5 microns square, the same proportion of light will be captured
by the sensor. But because smaller pixels have less dark current, a
system with smaller pixels can in practice perform better at low light
long exposure photography.
For example, consider a 600 mm f/5.6 lens with a digital camera having
8 micron pixels. Call this System A. The angular size of one pixel is
2.75 arc-seconds (this is called the
plate scale). The lens diameter is 600/5.6 = 107 mm. Consider a
second system, System B, with a 300 mm f/2.8 lens and a digital camera
with 4-micron pixels. System B has the same lens diameter (300/2.8=) 107
mm, and the same plate scale of 2.75 arc-seconds per pixel. The lens in
Systems A and B will each deliver the same amount of light to the pixel.
Assuming the image quality of the two lenses is the same, both will
produce equal images in the same exposure time, EXCEPT in long exposures
where noise from dark current is a factor (deep space astrophotography).
This is where the smaller pixels have an advantage.
The next thing to consider in astrophotography is plate scale for imaging
different deep space objects. A few objects are quite large, like
the Great Nebula in Orion, M31, which is about double the diameter of the full Moon,
the the Andromeda galaxy, M31, which is over 8 times wider than the full Moon.
There are also some larger structures of the Milky Way that can be imaged
by shorter focal length lenses. There are also many smaller objects, including
galaxies and nebulae, which require finer resolution to get much detail
in them. But atmospheric turbulence limits resolution in most cases except
in rare circumstances. Long exposure astrophotography is often limited to
about 2 arc-seconds. The image in Figure 10 is at 2-arc-seconds per pixel and if you
follow the link to the gallery image, you will see a larger image at 1.5 arc-seconds per pixel.
See;
Astrophotography and Focal Length: What Can You Image with Various
Lenses? for more examples.
For deep sky astrophotography, I usually choose lens and sensor to give
between 1 and 4 arc-seconds per pixel depending on the size of the object.
For nightscapes, it can be more about field of view and larger structures,
so plate scales in the tens of arc-seconds per pixel are chosen.
A 200 mm lens on a camera with 4 micron pixels gives 4.1 arc-seconds per pixel,
and 800 mm gives 1 arc-second per pixel. See
plate scale for scales with specific cameras and lenses.
See
Lens Field of View for data on camera sensor sizes and lenses.
Discussion and Conclusions
Putting the above information together, the ideal astrophotography
system is very fast lenses feeding cameras with small pixels for a given
plate scale. As with nightscape photography, where lenses like 24 mm
f/1.4 and 35 mm f/1.4 are ideal, moving up the angular resolution range,
50 mm f/1.4, 85 mm f/1.4, 100 mm f/2, 135 mm f/2, 200 mm f/2 or f/2.8,
300 mm f/2.8, 400 mm f/2.8, 500 mm f/4 feeding digital cameras with
pixel sizes around 4 microns are ideal.
Wide angle lenses, like 15 mm f/2.8 can make for easy night sky images.
But the small apertures mean little light is gathered. A 15 mm f/2.8
has a smaller aperture diameter (5.4 mm) than the dark adapted human
eye (about 7 mm). The little light gathered by such lenses results in
a lot of noise in the typical 20 to 30 second exposures typical done
by nightscape photographers. That noise is confused with stars leading
people to think they have too many stars in their images. Larger aperture
lenses, like 24 mm f/1.4, 35 mm f/1.4 collect many times more light,
producing images with less noise. The less noise shows faint stars
better, making for a better balance of stars and Milky Way clouds (see
Figure 3c). Mosaics made with these larger aperture lenses make cleaner
images with more detail, higher contrast and greater impact.
Another take-home message from this article and the physics: use the largest
aperture lens/telescope to collect the most light. Efficiency may mean
doing a mosaic depending on available resources of lens aperture size,
focal lengths and fields of view. One can compromise on the lens for
simplicity (e.g. ultra-wide lens and single short exposure versus
mosaic with a larger aperture lens), but that simplicity reduces light
collection, increasing apparent noise and resolution. This is true
for daytime as well as nighttime photography--the physics does not
change, just in daytime photography there is generally more light so
the compromise may result in an acceptable image.
See Recommended Cameras and My Gear List for
Photography for specific cameras and lenses that I use, and watch here for
recommendations of the best cameras and lenses for night and astrophotography
for Canon, Nikon and other manufacturers.
Technical. The technical term for the above concept of lens aperture collects
the light and the field of view of the pixel is called the Etendue. It is the fundamental
property of imaging systems. See my series on
Understanding Exposure for more information.
If you find the information on this site useful,
please support Clarkvision and make a donation (link below).
References and Further Reading
Clarkvision.com Nightscapes Gallery.
Clarkvision.com Astrophoto Gallery.
The Night Photography Series:
















